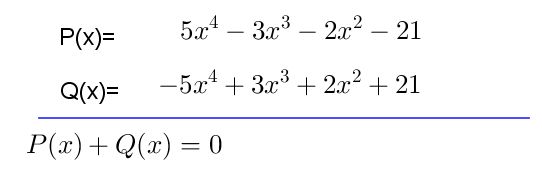Antes de comenzar a sumar polinomios es importante que recuerdes sumar números enteros, esto te ayudará a comprender mejor ´para realizar estas operaciones algebraicas. Si quieres tener éxito resolviendo adición de polinomios debes conocer los pasos a seguir para la resolución de ejercicios, además de manejar las operaciones básicas, suma y resta de fracciones con igual y diferente denominador, y reconocer cuando los términos son semejantes.

Suma de polinomios en la vida diaria

¿Sabes cómo identificar cuando los términos son semejantes? Dos términos son semejantes cuando tienen la misma variable o parte literal y el mismo exponente. Por otra parte, si buscas la aplicación de los polinomios en la vida diaria, es interesante que observes tu entorno, podrás ver cómo hay variables en todos lados. Por ejemplo, cuando vas al supermercado y agrupas frutas con frutas y verduras por verduras, estás relacionando términos semejantes.

Para realizar la suma de dos o más polinomios, se debe sumar los coeficientes de términos cuyo factor literal sean iguales,es decir las variables y exponentes(o grados) deben ser los mismos en los términos a sumar.

Propiedades de la suma de polinomios.

1. La suma de dos o mas polinomios nos da otro polinomio.
2. Propiedad asociativa. A(x)+B(x)+C(x)=(A(x)+B(x))=A(x)=A(x)+(B(x)+C(x))
3. Elemento neutro A(x)+0=0+A(x)=A(x) en este caso si le sumas cero a un polinomio,sigue dando cero,con el énfasis de que aquí cero se le llama el polinomio nulo
4. Propiedad conmutativa A(x)+B(x)=B(x)+A(x) da el orden de los sumando el resultado por lo tanto el resultado no se altera.
5. Existencia del elemento opuesto si A(x) le sumamos su opuesto –A(x) el resultado es cero.

La suma es una operación que tiene por objeto reunir dos o mas expresiones algebraicas (sumandos) en una sola expresión algebraica (suma).

Suma de polinomios

Sumar a-b,2a+3b-c y -4a+5b la suma puede indicarse incluyendo los sumandos dentro del paréntesis;

Así: (a-b)+(2a+3b-c)+(-4a+5b).

Ahora colocas todos los términos de estos polinomios. A continuación,  de otros con sus propios signos, y tendremos:

a-b+2a+3b-c-4a+5b=-a+7b-c. 

Es importante colocar los polinomios unos debajo de los otros de modo que los términos semejantes queden en columna; se hace la reducción de éstos, separándolos unos de otros con sus propios signos. Finalmente se suman o restan según sea el caso.

Para sumar polinomios debes ordenarlos en forma decreciente o creciente, colocar los polinomios uno debajo del otro, de manera que los términos semejantes queden en la misma columna, dejando un espacio si falta una potencia de x, o se completan con ceros los términos que faltan y sumar algebraicamente los coeficientes de los términos semejantes.

Los polinomios se pueden sumar de la siguiente manera:

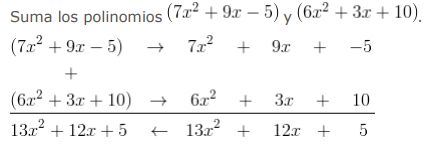
Los términos de los polinomios se alinearon, uno encima del otro, observa que el signo negativo -5 se mantuvo encima del 10. Debes tener mucho cuidado al sumar números enteros.

Otra manera de sumar polinomios es de la siguiente manera:

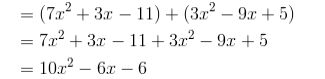
Otra de las formas de resolver esta operación es de forma horizontal, así que puedes sumar -11+5. Lo recomendable es seguir los siguientes pasos:

Paso #1 Escribir sin paréntesis

Paso #2 Combinar términos semejantes

Puedes ver que en el paso 1 el polinomio puedes  escribirlo sin paréntesis porque los paréntesis sirven sólo para
mostrar la separación de los polinomios. Ten cuidado y ubica los términos semejantes correctamente. Aunque muchos estudiantes no se sienten cómodos con este método también se recomienda, con mucha práctica se hará más fácil resolver.

Ejemplo#1 Sumar los polinomios P(x)+Q(x)

Antes de solucionar el siguiente polinomio, debes seguir los siguientes pasos

Paso#1 Identifica el grado del polinomio, recuerda que es el mayor exponente que posee la variable. Una vez identifique el grado del polinomio, revisa que esté completo, es decir que tenga todos los términos hasta llegar al grado.

Paso #2 Si el polinomio está incompleto deberás completarlo con 0x elevado al exponente faltante

Paso #3 Ordena los polinomios P(x) y Q(x)  en forma decreciente, es decir de mayor a menor.

Paso #4 Una vez has organizado ambos polinomios ya puedes sumar, recuerda que signos iguales se suman y signos diferentes se restan.

Paso #5 Ten en cuenta que al sumar polinomios se mantiene la misma variable y el mismo exponente. Observa el ejercicio resuelto.

 

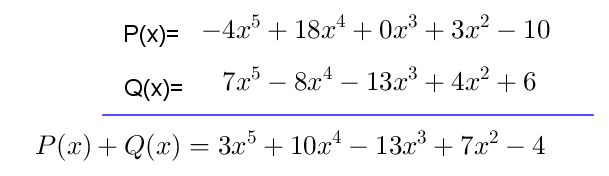
Ejemplo#2 Sumar los polinomios P(x)+Q(x)

Paso #1 Solicitan que sumes los polinomios P(x) y Q(x). Si observas el polinomio P(x) está ordenado y el grado del polinomo es 3, esto indica que debe completarse  P(x) con respecto a Q(x) y ordenarse  en forma decreciente.

Paso #2 Una vez has ordenado el polinomio P(x), es momento de observar el polinomio Q(x)  el cual es de grado 4 y está completo, también está ordenado en forma decreciente.

Paso #3 Cuando ya esté ordenado el polinomio P (x) y Q(x) ya puedes comenzar a sumar, ten en cuenta que se suman los coeficientes y se mantiene la misma variable y el mismo exponente.

Paso #4 Finalmente, obtienes el resultado final

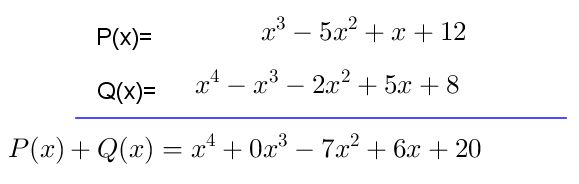
Ejemplo #3

Sumar el siguiente polinomio verticalmente

Solución:

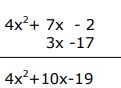
Para resolver este polinomio de grado 2 se ordenó en forma decreciente y se sumó en forma vertical. Para realizar este tipo de ejercicios ten en cuenta que signos iguales se suman y se coloca el mismo, y signos diferentes se restan y se coloca el signo del número mayor.

Ejemplo#4 Sumar los polinomios P(x)+Q(x)

Paso #1 Solicitan que sumes los polinomios P(x) y Q(x). Si observas el polinomio P(x) está ordenado y el grado del polinomo es 4, esto indica que debe completarse  P(x) con respecto a Q(x) y ordenarse  en forma decreciente.

Paso #2 Una vez has ordenado el polinomio P(x), es momento de observar el polinomio Q(x)  el cual es de grado 4 y está completo, también está ordenado en forma decreciente.

Paso #3 Cuando ya esté ordenado el polinomio P (x) y Q(x) ya puedes comenzar a sumar, ten en cuenta que se suman los coeficientes y se mantiene la misma variable y el mismo exponente.

Paso #4 Finalmente, obtienes el resultado final que es cero. Se evidencia la propiedad de la adición del  elemento opuesto si A(x) le sumamos su opuesto –A(x) el resultado es cero.

Ahora que ya sabes sumar polinomios, puedes poner en prácticar y reforzar tu aprendizaje en esta hermosa asignatura. ¡Manos a la obra!