¿Sabes cómo factorizar por Ruffini? Esta regla es un algoritmo que permite factorizar fácilmente, además de permitir calcular más rápido la división de un polinomio entre un binomio. Es importante tener en cuenta que la factorización por Ruffini consiste en escribir los polinomios en forma de factorización, para ello debes seguir los pasos de forma correcta. Verás que es muy fácil y de gran utilidad en tus clases de matemáticas.

¿Para qué sirve factorizar un polinomio?

Sirve para encontrar los “ceros “o “raíces “. En división tenemos para analizar la posibilidad y la negatividad en la factorización o para encontrar los máximos y/o números en la factorización de polinomios se puede utilizar para resolver inecuaciones de grado 2 o mayor, hallar algunas líneas, resolver ecuaciones, trigonométricas, es decir que sirve para factorizar porque en otros términos se requiere de factorizar polinomios, suma algebraica con multiplicación en vez de suma y resta.

Es importante también saber si ya has factorizado en un ejercicio y lo puedes saber de la siguiente manera:

• Multiplicas  los factores que obtuviste, con esto se logra elegir a la misma y/o resta de la que pertenece.
• Al factorizar estás obteniendo una expresión equivalente a su original, pero en forma de multiplicación.

También es importante que tengas en cuenta que un factor común el mismo es “algo”, numérico, letra, “una expresión algebraica” que está multiplicando en todos los términos. Tiene que estar en todos los términos, por eso es “común” (común a todo), también se le llama factor a los números que están multiplicando de lo que resulta de dos palabras “factor” y “común”.

Pasos para factorizar por Ruffini

1. Ordenar el polinomio en orden decreciente, en caso de que falte algún término dejamos el espacio o colocas cero ya que el polinomio debe estar completo.
2. Debes tomar en cuenta que tenga término independiente; sino lo tiene debe sacar factor común hasta conseguir el término independiente.
3. Buscar todos los divisores del término independiente.
4. Formar una tabla y colocar los coeficientes del polinomio.
5. Colocar el primer divisor o raíz que se quiera usar en la esquina inferior izquierda, y haga el primer coeficiente tal cual esté.
6. Para la selección de división debemos tener presente que los números que vamos obteniendo o bajando los vamos a multiplicar por el divisor y luego el resultado, lo vamos a sumar o restar con los coeficientes que tenemos; el divisor que se escoja debe ser un número que haga que al final nos dé resto cero para saber su número es raíz, es sustituyendo en el polinomio ese número como el valor de la variable (x), y si da cero (0) es raíz, sino da cero no lo es y se pasa al siguiente divisor.

Al obtener la primera raíz el proceso se repite con los nuevos coeficientes obtenidos hasta que nos quede un solo coeficiente o hasta que no exista ninguna raíz que haga que nos de cero (0).

Ejercicios resueltos de factorización por Ruffini

Ejemplo # 1

3x²+9x+6

Solución:

El polinomio esta ordenado completo y tiene término independiente los divisores de termino independiente.

D(6)=±1,±2,±3,±6 bajamos los coeficientes y formamos la tabla.

Se probó con el (+1) y dio resto igual a (18) porque (1*3=3) (3+9=12) (1*12=12) (12+6=18), por lo tanto ese divisor no sirve.

Es importante resaltar que la factorización de polinomios consiste en escribir los polinomios en forma de factores.

Para factorizar un polinomio debemos sacar factor común si se puede comprobamos si es una ecuación de segundo grado verificamos si no resulta ecuación de segundo grado y aplicamos Ruffini.

Ejemplo # 2

Paso # 1 Buscar los divisores del término independiente en este caso es el número (2)

Divisores:

Paso # 2 Apliquemos la regla de Ruffini y en círculos se resalta las raíces

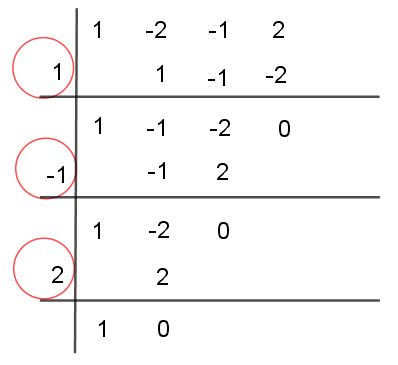
Paso # 3 Transformamos las raíces en factores, como son 3 raíces se obtiene 3 factores con signos opuestos, quedando así:

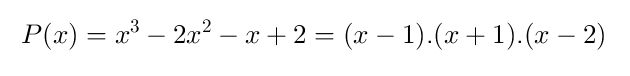
Ejemplo # 3 aplicando factorización por Ruffini paso a paso

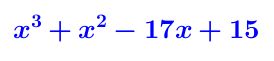
Paso #1 Observa si la expresión algebraica está completa y ordenada en forma decreciente. Si es así, procede a organizar en la tabla para aplicar la Regla de Ruffini. Seguidamente hallar los divisores de 15, como 5 es uno de ellos, se toma -5, tal como lo observas en la imagen.

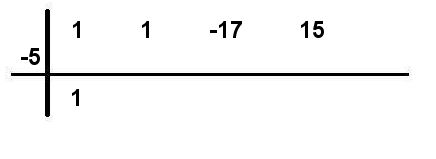
Paso #2 Continúa multiplicando (-5) por 1, el resultado que es -5 lo sumas con 1, tal como lo ves en la imagen. Repites el procedimiento hasta encontrar la primera raíz.

Paso #3 Repite el mismo proceso multiplicando (-5) (-4), luego sumando el resultado con 20, tal como lo ves en la imagen.

Paso #4 Como ya obtuviste el último resultado cero continúas hallando la siguiente raíz.

Paso #5 Continúas hallando las siguientes raíces.

Paso #6 Seguidamente se halla la tercera raíz

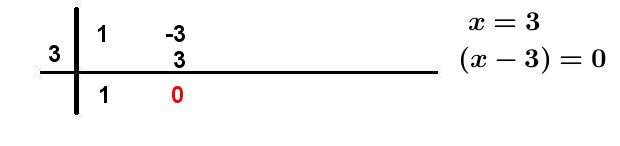
Paso #7. Finalmente, la expresión factorizada queda de la siguiente manera:

Ejemplo #4

    x²+x-2

Paso#1 Determina los coeficientes del polinomio a factorizar

Paso#2 Comienza probando con los divisores que en este caso es el número 2. Como puedes ver en la imagen se comienza probando con -2 el cual se multiplica por 1 que es el primer coeficiente del polinomio

Paso#3 Se suman o restan en columnas. Si al operar el último coeficiente y éste resulta cero, entonces has encontrado la primera raíz.

Paso #5 Repite el procedimiento.

Paso#6 Finalmente, obtienes: (x+2) (x-1) que corresponde al polinomio factorizado.

Consejos para conseguir las raíces y factorizar por Ruffini de forma rápida

Seguramente para ti ha sido complicado hallar las raíces al factorizar por Ruffini y ha sido tu dolor de cabeza, ya no tienes porque preocuparte, ahora puedes seguir los siguientes consejos y ya verás que irá mejor.

1. Si la suma de los coeficientes da cero, como por ejemplo: 1, 6, 5 y -12, eso quiere decir que se puede probar con el 1 y el resultado sería como lo ves en la imagen.

2. El segundo truco es que si el número no funciona ya no servirá en los que sigue de Ruffini, por lo que se puede tachar y no se pueden probar en los siguientes pasos del polinomio

3. Lo ideal es que comiences probando con los números más pequeños, ya sean positivos o negativos, debido a que los grandes es posible que desaparezcan como opciones en lo que sigue de Ruffini

4. Ten en cuenta que si todos los coeficientes son negativos, las raíces serán negativas