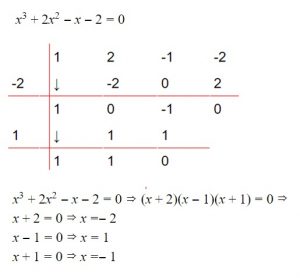¿En qué consiste rufinizar?
Rufinizar es una método que se utiliza para realizar la división de un polinomio P(x) entre un monomio del tipo x + a, siendo “a” cualquier número entero.
Si la división del polinomio P(x) entre un monomio x + a es exacta, podemos afirmar que x + a es una raíz del polinomio, y así, podemos factorizar si es lo que se necesita realizar.
¿Cómo se rufiniza?
Vamos a aprender a rufinizar con el siguiente ejemplo:
![]()
Lo único que vamos a realizar en estos momentos es la división, más tarde, veremos de qué forma es útil en las ecuaciones.
Lo haremos mediante pasos sencillos:
Es importante tener ordenado el polinomio para evitar errores, es decir, las incógnitas elevadas a mayor exponente deben estar al principio del polinomio, de la forma en la que está escrita el ejemplo (al principio).
![]() Es importante que a la hora de rufinizar después de haber ordenado el polinomio, el último número no esté acompañado de una incógnita. En el caso de que sí vaya acompañado de una, nos da una pista de que se deberá sacar factor común.
Es importante que a la hora de rufinizar después de haber ordenado el polinomio, el último número no esté acompañado de una incógnita. En el caso de que sí vaya acompañado de una, nos da una pista de que se deberá sacar factor común.
Después de realizar todo esto, ya podemos empezar a rufinizar, lo primero que haremos, es dibujar las siguientes líneas.
 Una vez que tengamos esto, debemos escribir en la parte superior derecha los coeficientes de cada término y el número sin incógnita en orden, sin olvidarnos de si son números positivos o negativos. En el caso de que no haya coeficiente, es decir, que se encuentre la incógnita sola, se entiende que es 1.
Una vez que tengamos esto, debemos escribir en la parte superior derecha los coeficientes de cada término y el número sin incógnita en orden, sin olvidarnos de si son números positivos o negativos. En el caso de que no haya coeficiente, es decir, que se encuentre la incógnita sola, se entiende que es 1.
Nota: Si la ecuación es como la siguiente, que no tiene monomio de algún grado, se pondría un 0 como coeficiente de ese monomio.
Nuestro ejemplo quedaría de la siguiente forma:

Como se puede apreciar, debajo del primer número es común poner una flecha, y en la parte de debajo de la línea horizontal, se pone el mismo número (solo con el primero).
Hay dos opciones a la hora de rufinizar:
- Que te den el polinomio para que lo dividas entre un monomio (del tipo x+a, como he mencionado antes) y el resto puedan ser varios números.
- Que vayas a factorizar el polinomio y quieres ayudarte con ruffini, y el resto tenga que ser 0 para que sea correcto a la hora de escribirlo factorizado.
En el primer caso, tendrás que poner en la parte superior izquierda el número entero (a) del monomio x+a, con el signo contrario.
Si ese no es el caso, deberás ir probando para ver si el resto es 0, los números que se deben probar para ver si se puede realizar, son los divisores del último dígito de los coeficientes en la tabla de Ruffini (en este ejemplo, el 8), los divisores de 8 son: +1, -1, +2, -2, +4, -4, +8, -8. En este caso, es o 2 ó -2, ahora veréis por qué.

Para seguir rufinizando, se deben multiplicar los números que hemos colocado en azul y poner el resultado donde se encuentra el número verde.
El siguiente, consiste es realizar la suma de los números en verde, es decir, el producto de la multiplicación anterior y el número que tiene en la parte superior.
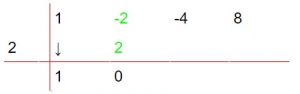
Los siguientes pasos ya son parecidos entre sí, el resultado de la suma (de los números en la parte superior derecha), debemos multiplicar por el número colocado en la parte superior izquierda de las líneas perpendiculares (el -a del monomio). De la siguiente forma (los números en azul son los que debemos multiplicar y el resultado de la suma, los números en verde son los resultados de la multiplicación y los que se suman):
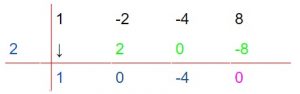
El cero está en morado porque es uno de los números más importantes de este método, es el resto de la división, si la división es exacta, además, también sabemos de qué forma factorizar el polinomio con el que hemos empezado el problema (como se ha nombrado antes).
Para saber qué monomio es el que hemos utilizado para dividir el polinomio:
![]()
solo se necesita cambiar el signo al número de la parte superior izquierda, y añadirle una x delante. En este caso, el monomio es x-2.
¿Y cuál es el cociente de la división?
Pues el cociente son los números que se encuentran en la parte inferior derecha sin contar el resto (escrito en morado), el último número de los inferiores, corresponde a un número sin incógnita, el de la derecha, a una incógnita elevada a 1, el siguiente a la derecha, a la misma incógnita elevada a 2…. Manteniendo los signos.
En este caso: ![]()
Por tanto:
![]()
En las divisiones exactas, el dividendo es igual al divisor por el cociente, por tanto, se cumple que:
Pero es importante, que a la hora de rufinizar, si lo que queremos hacer es sacar factor común, no nos olvidemos si podemos seguir rufinizando, como en este caso. No obstante, no siempre se puede.
Se repiten los mismo pasos que antes:
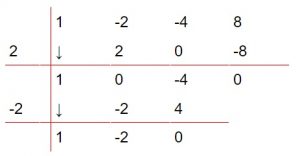
Ahora, se puede afirmar que:
![]()
Esta operación puede parecer una simple división de un polinomio entre un monomio, pero como he ido diciendo, esto puede llegar a ser muy útil en otros casos, como en la hora de simplificar una fracción con incógnitas o para resolver ecuaciones de un grado mayor que 2, pues este método, nos ayuda a factorizar los números.
Vamos a ponernos en el caso de que el polinomio que he puesto en un primer ejemplo estuviera igualado a 0, en una ecuación:
![]()
A continuación os dejamos un ejemplo que podéis realizar y así saber si habéis aprendido cómo se rufiniza. Tenéis además el resultado más abajo.