Aunque a muchos estudiantes se les dificulta la multiplicación de monomios, realizar este tipo de ejercicios realmente es muy sencillo sólo debes conocer operaciones básicas y manejar muy bien las propiedades de la potenciación, especialmente las multiplicación de potencia de igual base.

Por otro lado, la multiplicación de monomios viene expresada de la siguiente manera k.x elevada a la n donde k es un número real y n es un entero positivo,  básicamente un polinomio con un solo término.

Cuando se multiplica dos monomios lo que vas hacer es multiplicar los signos en primer lugar, luego los coeficientes y por último la variable. Esto significa que el producto de un monomio por un monomio resulta otro monomio, resultando como coeficiente el producto de ambos monomios.

Para multiplicar monomios se multiplican los coeficientes y la parte variable (literal) por separado, aplicando la ley de los signos y propiedad de la potenciación. Para resolver los ejercicios con polinomios se aplica la propiedad distributiva antes de multiplicar los monomios. Un monomio  es una expresión algebraica que consta de un solo término como lo es: 8b ⁴

Regla para multiplicar monomios

Se multiplica los coeficientes y a continuación de este producto se escribe las letras de los factores en orden alfabético y colocándole a cada letra un exponente igual a la suma de los exponentes que tenga en los factores, el signo del producto se dará ya por la ley de los signos.

Ejemplo:

(2a ³)(-3a ³)=-6a ⁶

El signo del producto es más (+) por menos (-) es igual a menos (-)

Multiplicación de polinomios por un monomio

Sea el producto (a+b).c multiplica (a+b) por c equivale a tomar la suma (a+b) como sumando c veces luego

(a+b)c=(a+b)+(a+b)+(a+b)…..veces =(a+b) +….veces )+(b+b+b….c veces )=ac+bc

Sea el producto (a-b)c tendremos (a-b)c(a-b)+(a-b)…c veces.=(a+a+a….veces)-(b+b+b….veces)=ac-bc..

Lo que debes tener en cuenta para multiplicar un polinomio por un monomio

• Se multiplica el monomio por cada uno de los términos del polinomio teniendo en cuenta en cada caso la regla de los signos y se separan los producto con sus signos correspondientes.
• Para la multiplicación es necesario hacer uso de la ley de los signos que dice:(+)(+)=(+) ,(-)(-)=(-),(+)(-)=(-),(-)(+)=(-)

Para la multiplicación se debe tener en cuenta la ley de los exponentes en la multiplicación de bases iguales los exponente se suman a elevado a la m.(nⁿ )=a^m+eⁿ

Monomio por monomio

La multiplicación de monomios se realiza multiplicando un monomio por otro monomio para obtener como resultado otro monomio.

(10a³b²c)(-3abc⁵ )= -30 a⁴b³c⁶

La multiplicación de monomios es otro monomio que tiene un coeficiente resultante que es el producto de los coeficientes y cuya variable se obtiene multiplicando las potencias que tengan la misma base y sumando los exponentes.

Procedimiento para multiplicar monomios.

• Multiplicación de monomios se multiplica los signos seguidamente de los coeficientes y por último los literales.
• Multiplicación de signos
• Al multiplicar signos iguales el resultado es positivo y signos diferentes el resultado es negativo, si el término no tiene signo indicado se sobreentiende que es más (+).
• Multiplicación de coeficientes: Se hace con el procedimiento conocido si el término no tiene exponente indicado el coeficiente se entiende que es uno (1).
• Multiplicación de literales: Aquí se suman sus exponentes si no tiene un exponente indicado se sobre entiende que es uno (1).
• Multiplicación de fracción: Se multiplica numerador con numerador y denominador con denominador.

Ejemplo:

Multiplicamos el siguiente monomio:

(4.5) se multiplican los signos (+) por (+) igual más (+) seguido a ello multiplicamos los coeficientes uno (4) por (5) igual (20) como se puede observar la parte literal no está indicada.

Ejercicios resueltos de multiplicación de monomios

Ejercicio #1

Paso # 1: Para resolver la multiplicación de monomios en primer lugar debes tener claro que se multiplica numerador por numerador y denominador por denominador.

Paso # 2: Procede a dejar la misma base que es el caso de la variable y suma los exponentes.

Ejercicio #2

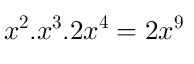
Paso # 1: Para resolver la multiplicación de monomios en primer lugar debes tener claro que se multiplica los coeficientes.

Paso # 2: Procede a colocar la misma base y se suman los exponentes

Ejercicios #3

Paso # 1: Para resolver este tipo de ejercicios de  multiplicación de monomios deberás multiplicar los coeficientes y signos en este caso son 1,1 y 2, todos positivos.

Paso # 2: Luego, colocas la misma base y sumas los exponentes.

Ejercicio #4

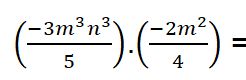
Solución:

Paso # 1: Para resolver la multiplicación de monomios en primer lugar debes tener claro que se multiplica numerador por numerador y denominador por denominador.

Paso # 2: Procede a dejar la misma base que es el caso de la variable y suma los exponentes.

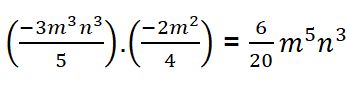
Ejercicio #5

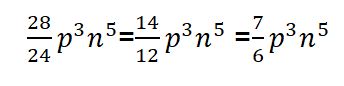
Paso # 1: Para resolver la multiplicación de monomios en primer lugar debes tener claro que se multiplica numerador por numerador y denominador por denominador.

Paso # 2: Procede a dejar la misma base que es el caso de la variable y suma los exponentes.

Ejercicio #6

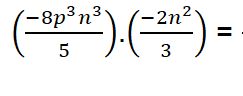
Paso # 1: Para resolver la multiplicación de monomios en primer lugar debes tener claro que se multiplica numerador por numerador y denominador por denominador.

Paso # 2: Procede a dejar la misma base que es el caso de la variable y suma los exponentes.

Ejercicio #7 Multiplique el polinomio P(x) y Q(x)

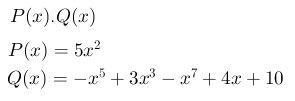
Paso#1 Se ordena el polinomio en forma decreciente y si no está completo se debe completar elevado al exponente faltante.

Paso#2  Se procede a montar en dos filas cada polinomio, de tal manera que quede organizado para poder multiplicar de forma sencilla:

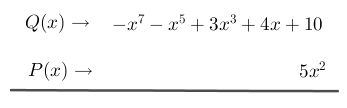
Paso #3 Se multiplica el monomio por el primer término del otro polinomio dando como resultado en este caso es

10. 5x²   

 

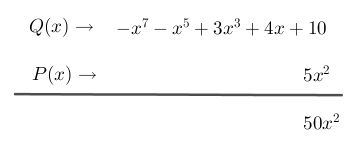
Paso #4 Continúa multiplicando  el monomio con el siguiente término del polinomio:

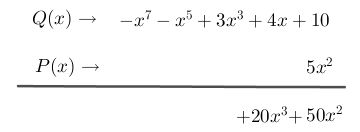
Paso # 5 Posteriormente, multiplicar el monomio por el siguiente término del polinomio, ten en cuenta que al multiplicar bases (variables) iguales debes sumar los exponentes.

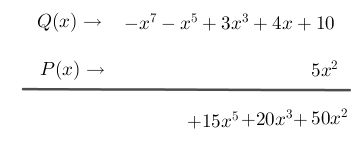
Paso # 6 Multiplicar el monomio por el siguiente término del polinomio:

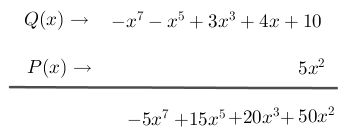
Paso # 7 Multiplicar el monomio por el siguiente término del polinomio:

Listo el resultado es:

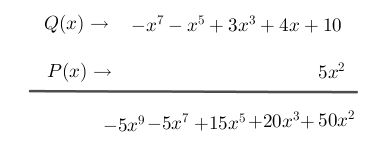
Como puedes ver la multiplicación de monomios es muy fácil, sólo debes poner en práctica los conocimientos básicos  aprendidos. Para ello, es muy importante reforzar tu aprendizaje en multiplicación de potencias de igual base, suma y resta con fracciones con igual y diferente denominador. No esperes más y pon manos a la obra para mejorar tus calificaciones en esta hermosa asignatura.