¿Te gustaría saber cómo sumar fracciones de forma sencilla? Para muchos estudiantes la suma de fracciones es un poco difícil, de allí la importancia de dejar muy claro el procedimiento para resolver y lograr excelentes resultados. Para resolver ejercicios de suma de fracciones deberás conocer si tienen igual o diferente denominador, luego eliges el procedimiento correcto para lograr la solución adecuada.

¿Te has preguntado qué es una fracción? Seguramente has escuchado que una fracción es una parte de un todo, aunque quizás pienses que sólo se trata de dos números separados por una línea. Esa parte de un todo representa diferentes situaciones en la vida cotidiana.

Para representar fracciones se expresa entre la relación de números naturales quedando de la siguiente manera: a/b, en el que a es la parte que se toma y b es el todo de la fracción.

Existen algunas situaciones de la vida cotidiana como por ejemplo repartos de herencias, tierras, bienes o el pago de tributos. Pero, hay casos más cercanos en los que se evidencian las fracciones como por ejemplo los que verás a continuación:

• Seguir instrucciones al elaborar una receta de cocina, se fraccionan los ingredientes.
• Cuando estás en el supermercado y compras un producto, como por ejemplo ½ litro de jugo de fresa, ¼ de libra de queso y ¾ libra de pollo
• En la fiesta de cumpleaños de tu mejor amigo puedes ver en cuantas partes cortan el pastel y la repartición en partes iguales a los invitados.

Sumar fracciones con igual denominador

Suma de fracciones con el mismo denominador en este caso el procedimiento es más sencillo, en vista de que solo se suman los numeradores y se mantiene el mismo denominador.

Ejemplo #1 

En este caso se mantiene el denominador (7) y sumar los numeradores que resulta 5.

Ejemplo #2

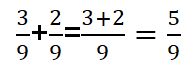
En este caso se mantiene el mismo denominador (9) y se suman los numeradores que resulta 5.

Suma de fracciones con diferente denominador

Para resolver suma de fracciones con distintos denominadores puedes resolver de dos maneras. A continuación, aquí tienes el primer caso llamado método de la cruz o carita feliz.

Resolviendo el mínimo común múltiplo (m.c.m)

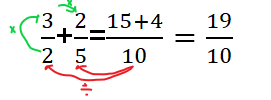
Se debe obtener el m.c.m (2,5) el cual es igual a 10. Para la suma de fracciones con distintos denominadores se puede hacer de dos maneras de forma directa y sacar el m.c.m del denominador, común múltiplo.

Sumar tres o más fracciones con el mismo denominador

El procedimiento es muy parecido al de la suma de fracciones de dos fracciones. Aquí solo sumamos los numeradores y colocas el mismo denominador. Observa el siguiente ejemplo, se deja el mismo denominador y se suman numeradores.

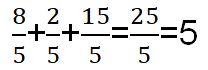
Ejemplo #2 Observa el siguiente ejemplo mantienes el mismo denominador y suma los numeradores.

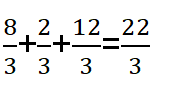
Suma de fracciones de tres o más con distinto denominador

Para sumar tres o más fracciones con diferente denominador, sigue los pasos a continuación:

Paso #1 Como puedes observar las fracciones tienen diferente denominador, por ello debes hallar el mínimo común múltiplo.

Paso #2 Una vez tengas el mínimo común múltiplo (m.c.m) procede a dividir entre cada denominador.

Paso #3 Una vez divides el mínimo común múltiplo entre cada denominador lo multiplicas por cada numerador.

Paso #4 Finalmente, sumas o resta según indique el ejercicio, en este caso sumas los numeradores manteniendo en el denominador el mínimo común múltiplo.

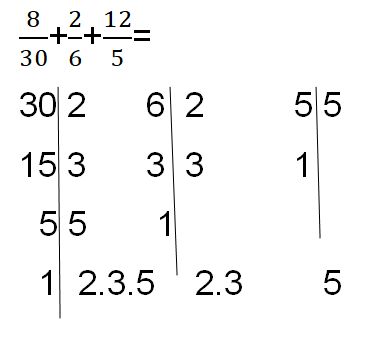
Paso #2  El m.c.m (30, 6,5)=30

Ejemplo #2

Paso #1 Como puedes observar las fracciones tienen diferente denominador, por ello debes hallar el mínimo común múltiplo.

Paso #2 Una vez tengas el mínimo común múltiplo (m.c.m) procede a dividir entre cada denominador.

Paso #3 Una vez divides el mínimo común múltiplo entre cada denominador lo multiplicas por cada numerador.

Paso #4 Finalmente, sumas o resta según indique el ejercicio, en este caso sumas los numeradores manteniendo en el denominador el mínimo común múltiplo.

Ejemplo #3 

Solución: 

Paso #1 Como puedes observar las fracciones tienen diferente denominador, por ello debes hallar el mínimo común múltiplo.

Paso #2 Una vez tengas el mínimo común múltiplo (m.c.m) procede a dividir entre cada denominador.

Paso #3 Una vez divides el mínimo común múltiplo entre cada denominador lo multiplicas por cada numerador.

Paso #4 Finalmente, sumas o resta según indique el ejercicio, en este caso sumas los numeradores manteniendo en el denominador el mínimo común múltiplo.

Suma de fracciones mixtas

¿Sabías que la suma de fracciones la vemos en la vida cotidiana? Entender las fracciones es muy importante ya que las tienes en todo lo que haces a diario.

Ten en cuenta que una fracción mixta está compuesta por un número entero y parte fraccionaria. A continuación, aquí tienes un ejercicio resuelto en el que hay  que resolver la fracción mixta.

Ejemplo #1

Paso #1 Convertir en fracción impropia cada una de las fracciones.

Paso#2 Luego, aplicar método de la carita feliz, ya que son de diferente denominador.

Paso #3 Finalmente, simplifica el resultado

Ejemplo #2

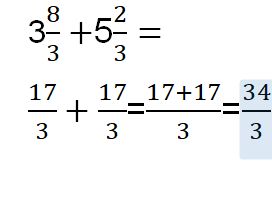
Pasos para resolver el ejercicio anterior:

Paso #1 Convertir en fracción impropia cada una de las fracciones.

Paso#2 Luego, como tienen igual denominador coloca el mismo denominador y sumas los numeradores.

Paso#3 Posteriormente, procede a simplificar si es necesario

Consejos para sumar de fracciones

Ahora que ya sabes resolver suma de fracciones de forma sencilla es importante que tengas en cuenta algunos consejos para que logres los mejores resultados en esta hermosa asignatura. A continuación, aquí tienes algunos trucos que te ayudarán en tus clases de matemáticas:

1. Cuando tengas una suma de dos fracciones observa los denominadores, en primer lugar, esto permitirá que apliques el método correcto y tendrás en cuenta si se trata de una suma de fracciones homogéneas o heterogéneas.

2. Si se trata de una suma de fracciones de diferente denominador elige el método que entiendas mejor, esto te ayudará a desenvolverte bien en los diferentes problemas que debas solucionar.

3. Si se trata de una suma de fracción de igual denominador no olvides que debes dejar el mismo denominador y sumar los numeradores.

4. Es muy importante simplificar la fracción resultante.

5. Ten en cuenta que los signos iguales se suman y se coloca el mismo signo, y signos diferentes se restan y se coloca el signo del número mayor.