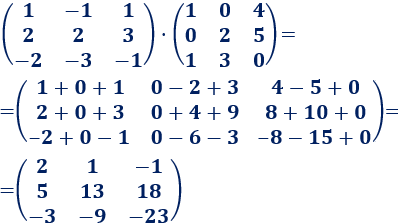
¿Quieres saber multiplicar matrices de forma sencilla? Para multiplicar matrices lo primero que debes tener en cuenta es que una matriz es un conjunto de elementos organizados por filas y columnas. En este artículo verás cómo hacerlo de manera sencilla y sin complicaciones con ejercicios resueltos paso a paso.

La multiplicación de dos matrices consiste en la unión de las matrices en un solo producto y suma de los elementos de las filas y columnas de las matrices origen, tomando en cuenta ordenar muy bien los factores. Para resolver la multiplicación de matrices de forma fácil es importante que  sigas paso a paso cada procedimiento.

Cómo multiplicar matrices de forma sencilla

Lo primero que debes tener en cuenta que puedes multiplicar matrices si son similares, esto significa que el número de columna de la primera matriz posee el mismo número de renglones de la matriz número dos. Es decir, si A es una matriz a x b  y B es una matriz b x c, entonces el producto resultante es a x c.

Cuando se resuelve multiplicación de matrices lo que se hace es multiplicar fila por columna en el que los elementos de la fila número uno de la Matriz A se multiplican por las entradas correspondientes de la columna. Por último los resultados se suman.

Matrices en la vida cotidiana

La multiplicación de matrices se utiliza en muchas situaciones de la vida cotidiana, tanto así que las puedes evidenciar para resolver muchas situaciones que se presentan a diario, especialmente en los casos de sistemas de ecuaciones lineales.

Por ejemplo, en informática las matrices son utilizadas ya que permite manipular información de manera sencilla, esto significa que son  ideales para representar gráficos y obtener resultados de cálculo numérico.

Ejercicios resueltos para multiplicar matrices de forma sencilla

Ejemplo #1

Sean las matrices A y B las siguientes:

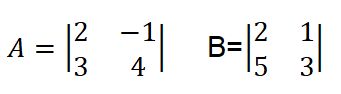
Determine A.B=

Paso #1: Para multiplicar la matriz A.B se multiplica la fila número uno por la columna uno y la columna número dos de la siguiente manera:

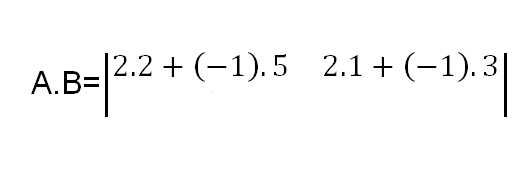
Paso #2 Seguidamente se multiplica la fila número dos por la columna número uno y por la columna número dos.

Paso #3 Luego, se procede a multiplicar en cada fila las operaciones planteadas en producto escalar.

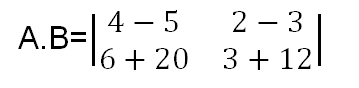
Paso #3: Una vez has multiplicado, procede a resolver las sumas y restas correspondientes en cada caso. Ten en cuenta los signos, esto significa que signos iguales se suman y se coloca el mismo signo y signos diferentes se restan y se coloca el signo del número mayor.

 

Ejemplo #2  Paso a paso para multiplicar matrices de forma rápida

Paso #1 Lo primero que debes hacer es multiplicar la fila de la matriz A por la primera columna de la matriz  B. Luego, se realiza el producto escalar, esto significa que multiplican los elementos de la fila y la columna.

Paso #2 Resuelve la multiplicación en cada fila, como lo ves a continuación.

 

Paso #3 Una vez tengas lista la primera fila procede a resolver la segunda fila, quedando de la siguiente manera:

Paso #4 Continúa resolviendo la operación, para este caso en la ´primera fila,  los signos iguales se suman , es decir resulta 14, y 1-9 signos diferentes se restan y se coloca el signo del número mayor, quedando -8 como resultado. Posteriormente, realiza el mismo procedimiento con la fila número dos.

Ejemplo # 3 Dadas las siguientes matrices A y B, determine  A.B=? Para este caso se tiene una matriz 3×3. Se resuelve de la misma manera que los ejemplos anteriores.

Paso# 1 En primer lugar, procede a multiplicar la fila número uno con la columna número, quedando de la siguiente manera: 2.5+4.2+2.6, esta operación queda asignada en la posición de la fila número, columna número 1. Luego, se toma la primera fila y la segunda columna, es decir, queda: 2.1+4.(-2)+2.3, ésta queda en la posición de la fila número uno columna número dos. Para concluir la primera fila, multiplicas la fila número 1 por la columna número tres, quedando de la siguiente manera: 2.2+4.2+2.(-3). Observa la siguiente imagen con el procedimiento explicado.

Paso #2 En segundo lugar, procede a multiplicar la fila número dos con la columna número, quedando de la siguiente manera: (-3).5+3.2+4.6, esta operación queda asignada en la posición de la fila dos, columna número 1. Luego, se toma la segunda fila y la segunda columna, es decir, queda: (-3).1+3.(-2)+2.3, ésta queda en la posición de la fila número tres columna número dos. Para concluir la tercera fila, multiplicas la fila número tres por la columna número tres, quedando de la siguiente manera: (-3).2+3.2+4.(-3). Observa la siguiente imagen con el procedimiento explicado.

Paso # 3 En tercer lugar, procede a multiplicar la fila número tres con la columna número, quedando de la siguiente manera: 1.5+(-2).2+2.6, esta operación queda asignada en la posición de la fila tres, columna número 1. Luego, se toma la tercera fila y la segunda columna, es decir, queda: 1.1+(-2).(-2)+2.3, ésta queda en la posición de la fila número uno columna número dos. Para concluir la primera fila, multiplicas la fila número 1 por la columna número tres, quedando de la siguiente manera: 1.2+(-2).2+2.(-3). Observa la siguiente imagen con el procedimiento explicado.

Paso #4 Es momento de multiplicar los productos en cada fila. Esto significa que  queda la primera fila de la siguiente manera: 10+8+12, 2-8+6, 4+8-6

Paso #5 Una vez resuelves la multiplicación la segunda fila queda de la siguiente manera: -15+6+24,-3-6+12,-6+6-12

Paso #6 Finalmente resuelves el producto de la tercera fila, resulta: 5-4+12, 1+4+6, 2-4-6. Observa en la siguiente imagen la operación en cada fila.

 

Paso #7 Una vez se efectúan los productos en cada fila, queda el último paso que es sumar o restar en cada fila. En este caso en la fila número 1, resulta: 30, 0, 6

Paso #8 Seguidamente realizas la operación en la segunda fila, quedando como resultado: 15, 3, -12

Paso #9 Finalmente, resuelves la fila número 3, la cual queda: 13, 11,-8. A continuación, observa la imagen:

Multiplicar matrices de una fila por una columna

Paso #1Para multiplicar una matriz de una fila por una columna, deberás seguir multiplicar cada elemento de la fila número uno por cada elemento de la fila número dos.

Paso #2 Seguidamente, procede a resolver los productos

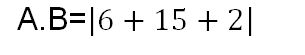
Paso #3 Finalmente procede a sumar, quedando como resultado: