¿Sabías que dividir por Ruffini es muy fácil? Sólo debes saber que la división utilizando esta regla viene dada por una expresión polinómica entre otro polinomio de tipo (x-a) usado en factorización.  Además, está formado por la suma o resta de varios monomios, un polinomio se puede dividir por un monomio o por otro polinomio.

Es una operación matemática y definida en el conjunto de los números naturales y los números enteros; en el caso de los números racionales, reales y complejos es siempre posible efectuar en la división, exigiendo que el divisor sea diferente.

Ejemplo # 1 División de un polinomio entre otro polinomio de la forma (x-a)

Paso # 1 Primero colocas la tabla donde reflejamos el valor de “a” es decir en valor del número que está restando x como divisor. “a” vale 1.

Paso # 2 Luego, se colocan los coeficientes de polinomio ordenados del mayor al menor grado. Los coeficientes son 1, de  x², 1 de x ∧ -2 del término independiente  -2.

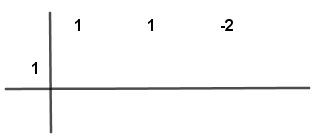
Paso # 3 El primer número de arriba lo copias debajo de la línea

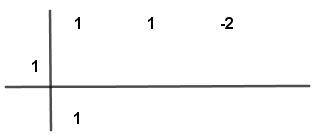
Paso # 4 Se multiplica el número por el valor de “a” (1) y el resultado se coloca bajo el segundo número de arriba.

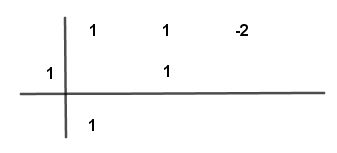
Paso # 5 Se suman los dos números y repites  la multiplicación expresando lo que dice la regla de Ruffini.

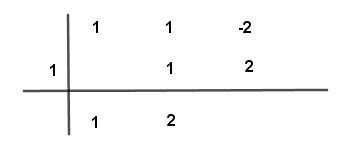
Paso # 6 Ahora, procede a sumar los dos últimos números y ponemos el resultado abajo lo que sera el resto de la división.

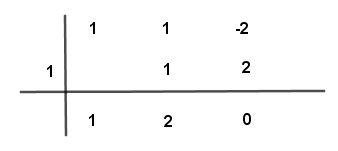
Paso # 7 Resultado

Cociente: x+2

Resto: 0

Se puede construir el polinomio cociente de la división.

En una división exacta de polinomios, el resto es igual a cero.

Dividir el polinomio D(x) entre el polinomio E(x) es hallar otro polinomio cociente C(x) tal que multiplicado por el divisor de el dividendo.

D(x)=E(x). C(x)

División exacta de polinomios.

Para dividir un polinomio por un binomio, se divide cada monomio del polinomio por el monomio, hasta que el grado del dividendo sea menor que el grado del divisor. El algoritmo es una versión generalizada de la técnica aritmética de división larga y se realiza fácilmente a mano, porque separa un problema de división complejo en otros más pequeños.

Condiciones de Divisibilidad 

La única condición para que sea posible es que el cociente dominante del monomiosea  de mayor grado. Además debes tener en cuenta que la división por Ruffini es fácil de elaborar y el más elegido por los estudiantes 

Ejemplo:

x-1(x-1) no causa problemas porque el coeficiente dominante es 1.

Ejemplo # 2 División de un polinomio entre otro polinomio de la forma (x-a)

Dividir

Paso # 1 Primero colocas la tabla donde reflejas el valor de “a” es decir en valor del número que está restando x como divisor. “a” vale 2.

Paso # 2 Luego, se colocan los coeficientes del polinomio ordenados desde el mayor al menor grado y completado con ceros. Los coeficientes son 1 de  x⁵ ,0 de x⁴ , 0 de x³ , -1 de x² , 3 de x ∧ 2 del término independiente 2

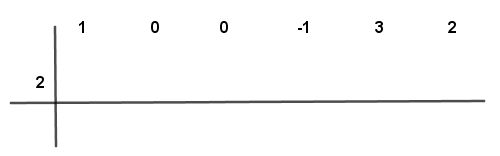
Paso # 3 El primer número de arriba lo copias debajo de la línea es decir el número uno (1)

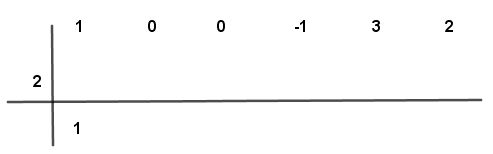
Paso # 4 Se multiplica el número por el valor de “a” (2) y el resultado se coloca bajo el segundo número de arriba.

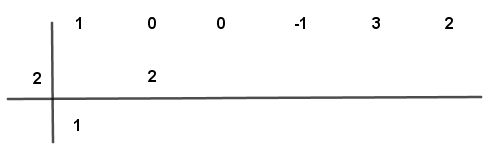
Paso # 5 Se suman los dos números cero y dos dando un resultado algebraico de dos.

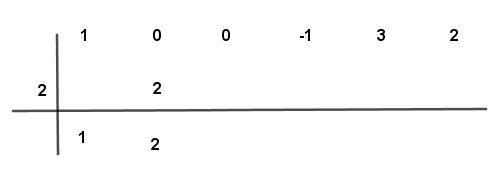
Paso # 6 Se multiplica el número por el valor de “a” (2) y el resultado se coloca bajo el segundo número de arriba

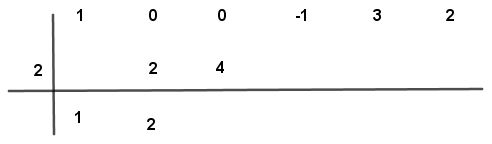
Paso # 7  Se suman los dos números cero y cuatro dando un resultado algebraico cuatro

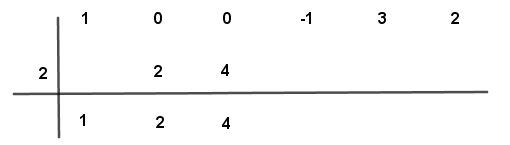
Paso # 8 Se multiplica el número por el valor de “a” (2) y el resultado se coloca bajo el segundo número de arriba

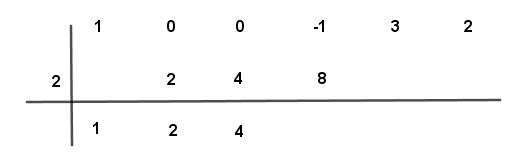
Paso # 9 Se suman los dos números  menos uno y ocho dando un resultado algebraico siete positivo

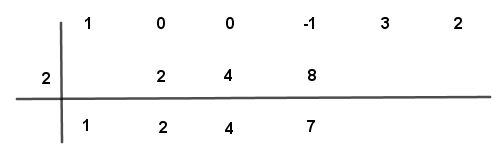
Paso # 10 Se multiplica el número por el valor de “a” (2) y el resultado se coloca bajo el segundo número de arriba

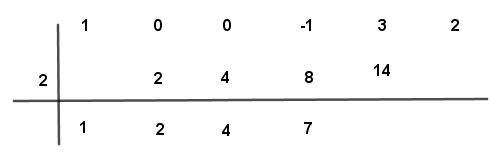
Paso # 11 Se suman los dos números  tres y catorce dando un resultado algebraico de diecisiete.

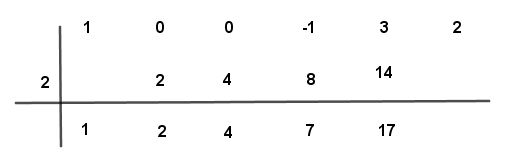
Paso # 12 Se multiplica el número por el valor de “a” (2) y el resultado se coloca bajo el segundo número de arriba

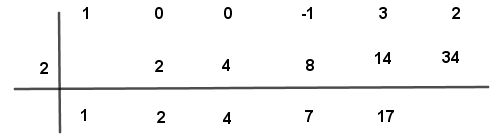
Paso # 13 Se suman los dos números  dos y treinta y cuatro dando un resultado algebraico de treinta y seis

Paso # 14 Finalmente, se obtiene:

Cociente:

Resto: 36

Ejemplo # 3 Dividir por Ruffini

Dividir por Ruffini cuando el divisor es de grado mayor que 1 y los exponentes de la variable del dividendo son múltiplos del exponente de la variable del divisor.

Determine el cociente y el resto de la división de:

Paso#1 Realizar un cambio de variable

Paso#2 Escribes el opuesto del término independiente del divisor

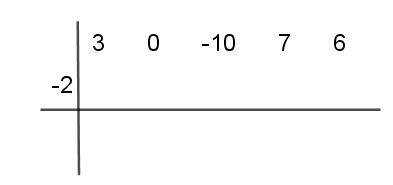
Paso # 3 El primer coeficiente del cociente, en este caso 3, se multiplica por (-2) y el producto resultante (-6) se suma al segundo coeficiente del dividendo, para obtener el segundo término del cociente. En este caso es -6

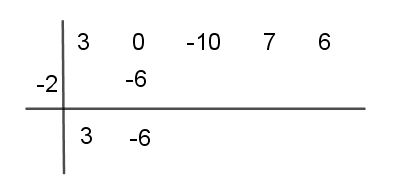
Paso # 4 La suma obtenida -6, la multiplicas por -2 y el producto resultante (12) se suma al siguiente coeficiente -10, obteniéndose 2

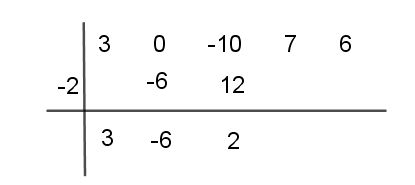
Paso # 5 Realiza la misma operaciones hasta obtener el resto

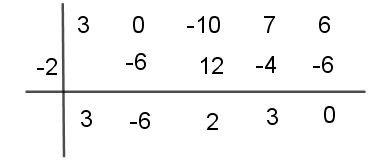
Paso # 6 Deshaces el cambio de variable y tendremos que el cociente vendrá dado por la expresión:

Paso # 7 Finalmente, se obtiene:

Cociente:

Resto: 0

Ejemplo # 4

Dividir por Ruffini cuando el divisor es de grado mayor que 1 y los exponentes de la variable del dividendo no son múltiplos del exponente de la variable del divisor.

Determinar el cociente y el resto de la división siguiente:

Solución:

Este caso debes descomponer la potencia de x en el dividendo, en el producto de dos potencias tales que una de ellas posea un exponente múltiplo de 3 y la otra un exponente un número menor que 3

Paso # 1 Ordenar primero el polinomio  dividendo en forma decreciente

Paso # 2 Realizar un cambio de variable, tal y como se realizó en el ejercicio anterior.

Si hacemos

Queda de la siguiente forma:

Paso # 3 Seleccionar el factor común a las potencias de “y”

Nota que los términos encerrados en los paréntesis no son más que los coeficientes de la variable

Paso # 4 Aplicar el método de Ruffini a la división anterior:

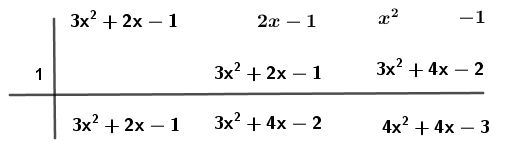
Paso # 5

El cociente de la división es
y

El resto es:

Si se toma el cociente de la división y regresamos al cambio de variable se tendrá que:

Quedándose así:

Luego el cociente es:

resto es: