Para realizar ejercicios de Ruffini, lo primero que debes conocer es su regla, quién fue Paolo Ruffini y cómo se comportó en cuanto a las matemáticas. Aunque para muchos estudiantes esta regla suele ser compleja, cuando se sigue los pasos correctamente el trabajo se hace más fácil.

¿Quién fue Paolo Ruffini?

Paolo Ruffini (1765 -1822) Matemático y médico nació en estados papales lo que hoy se conoce como Italia, fue profesor de matemáticas en la universidad de Módena de 1788 y despedido por negarse a jurar lealtad a Napoleón Bonaparte. Posteriormente, en el año 1799 fue readmitido y en 1806 recibió la cátedra de matemáticas aplicando a la escuela militar de Módena en 1814, nombrado director de la Universidad de Módena y en 1816 presidente de la sociedad Italia Dei Quaranta.

Estableció un método que se dio a conocer como Regla de Ruffini para realizar divisiones y otros aportes importantes de las matemáticas que nos permite entender la Regla de Ruffini como un método que nos ayuda a hacer cálculos matemáticos, ecuaciones de tercer grado o mayor, división de polinomios entre binomios y polinomio que sean de la forma x-a.

Ejercicios de Ruffini para Factorizar polinomios

También con esta regla se pueden hacer ejercicios de Ruffini como factorizar polinomios de tercer grado o mayor y calcular raíces de polinomios de grado mayor o igual a 3.

¿Para qué sirve la regla de Ruffini? Ayuda a facilitar el cálculo rápido de la división de cualquier polinomio entre un binomio  de la forma (x-r). Por otro lado, el método de Ruffini – Horner en cuanto a hallar el valor aproximado de la raíz de un polinomio  fue publicado con algunos años de diferencia por Paolo Ruffini (1804-1807- 1813) y por William George Horner (1819-1845) quien al parecer no tenía conocimiento de los trabajos publicados por Ruffini.

Casos especiales de los ejercicios de Ruffini

Existen casos especiales en la división de polinomios entre un binomio de forma x-a, siendo a cualquier número real. Paolo Ruffini, fue el primero en demostrar que la ecuación de quinto grado no se podía resolver por radicales.

En los ejercicios de Ruffini es muy utilizada la regla de Ruffini para realizar ejercicios de transformación de un polinomio en un producto de factores. Para realizar los ejercicios se obtiene la solución entera si la ecuación tiene soluciones complejas o reales, el método no es válido.

Es importante resaltar que por medio del algoritmo que es el conjunto ordenado de operaciones sistemáticas que permite hacer un cálculo y hallar la solución de un tipo de problemas, que ayuda a  obtener raíces de un polinomio y es de gran utilidad ya que para grado mayor que 2 no se dispone de fórmulas, al menos fáciles para poder obtenerlas.

A continuación, verás algunos conceptos que son de mucha importancia al momento de realizar los ejercicios, lo podemos llamar también términos matemáticos tales como:

• Coeficientes: Son números o parámetros que se escriben a la izquierda de una variable o incógnita que indica el número de veces que este debe multiplicarse.
• Variable: Quiere decir que está sujeto a cambios frecuentes o probables.
• Incógnitas: Es la variable que interviene en una ecuación o inecuación y que se verifica para unos valores determinados y se representa con las letras x, y, z, v, t etc.
• El grado del cociente: Es una unidad inferior al grado del dividendo.
• El resto: Es siempre un número.

Conocer las características del polinomio permite la obtención de las raíces de polinomios, Ruffini también demostró aunque no con mucha exactitud que no existe una fórmula para obtener las raíces de las ecuaciones de grado mayor o igual a 5.

Por otro lado, consiste en escoger una posible raíz y desarrolla una tabla, si el último resultado de la tabla es igual a 0 el procedimiento habrá finalizado correctamente, de no ser así se debe probar con otra raíz.

Para resolver ejercicios de Ruffini se establece un método para la división de polinomios entre el binomio para obtener el cociente  y el resto.

1. Se trazan dos líneas a manera de ejes y se escriben los coeficientes del polinomio ordenados sin omitir términos nulos se escribe la raíz R del lado izquierdo (invirtiendo el signo de este) y el primer coeficiente en el signo inferior.
2. Se hallan los divisores del término independiente  y se toman positivos y negativos. En este caso se comienza probando  con cada uno, el cual multiplicará al primer coeficiente del polinomio dado que quedará por debajo de la línea.
3. Se suman los dos valores obtenidos en la misma columna
4. El proceso se repite.

Los valores de V son los coeficientes del polinomio, resultando de R(x) de grado uno menor que el grado de P(x). El resultado es S.

Ejercicios resueltos

1. Dado el siguiente polinomio

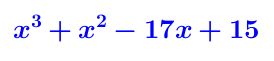
Paso # 1 Traza dos líneas a manera de ejes y se escriben los coeficientes de P(x) ordenados sin omitir términos nulos.

Paso #2. Se hallan los divisores del término independiente (15) y se toman positivos y negativos. En este caso se comienza probando  con -5 el cual multiplicará al primer coeficiente del polinomio dado que quedará por debajo de la línea, el cual es 1

 

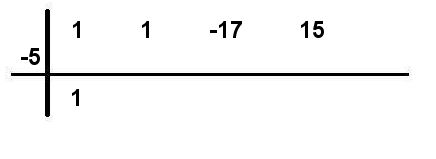
Paso #3. Se multiplica (-5) (1) quedando como resultado -5 por encima de la línea, luego sumas los dos valores obtenidos como lo observas en la imagen

Paso #4. Se repite el paso anterior

Paso #5. Continúan restando el último término y como es cero (0) obtienes la primera raíz.

Paso #6. Se repite el mismo procedimiento para los términos algebraicos resultantes en el paso anterior

Paso #7. Se suman los dos valores obtenidos en la misma columna

Paso #8. Continúan restando el último término y hallando la segunda raíz

Paso #9. Se repite el mismo procedimiento para los términos algebraicos resultantes en el paso anterior

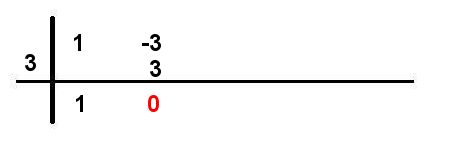
Paso #10. Finalmente se obtiene la última raíz

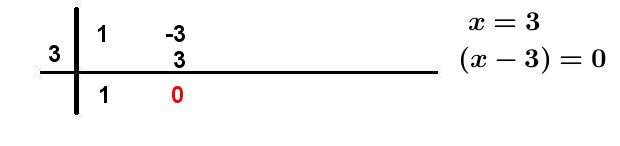
Paso #11. Finalmente, el polinomio factorizado queda de la siguiente manera:

Ejercicios de Ruffini #2

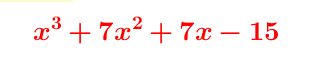
Paso# 1. Traza dos líneas a manera de ejes y se escriben los coeficientes de P(x) ordenados sin omitir términos nulos se escribe la raíz R del lado izquierdo

Paso #2. Se hallan los divisores del término independiente (15) y se toman positivos y negativos. En este caso se comienza probando  con -5 el cual multiplicará al primer coeficiente del polinomio dado que quedará por debajo de la línea, el cual es 1

Paso #3. Se repite el mismo procedimiento para los términos algebraicos resultantes en el paso anterior

Paso #4. Se repite el mismo procedimiento para los términos algebraicos resultantes en el paso anterior

Paso #5. Finalmente se ha resuelto otro ejercicio resuelto del polinomio factorizado queda de la siguiente manera: