¿Sabes cómo resolver multiplicación de polinomios? Resolver ejercicios de estos casos es muy fácil, lo único que debes hacer es seguir algunos pasos y conocer las propiedades de la potenciación, en especial multiplicación de potencia de igual base, claro está saber la tabla de multiplicar y dominio de operaciones básicas

En los empaquetados puedes ver casos de este tema de álgebra, por ejemplo cuando es necesario transportar muchas unidades de un mismo producto, es conveniente empaquetarlos con el mayor rendimiento posible. La forma de algunos objetos permite empaquetarlos con huecos, como las cajas de cereal, la crema dental.

Por ejemplo si se desea empaquetar 18 latas de leche condensada de radio x y altura 2x en una caja de cartón. Entonces el largo de la caja tendría que ser 2x.6=12x, el ancho mediría 2x.3=6x y la altura sería la de las latas 2x

Multiplicación de una constante por un polinomio

La propiedad distributiva con respecto a la adición se aplica cuando uno de los factores es una suma con dos o más sumandos; consiste en multiplicar cada uno de ellos por el otro factor para luego sumar estos productos.

Producto de un binomio por un polinomio

Para multiplicar un polinomio por un monomio se realiza multiplicando el monomio por cada uno de los términos del polinomio. 

Pasos para efectuar la multiplicación de un monomio por un polinomio:

• Se ordena el polinomio de forma decreciente
• Se aplica la propiedad distributiva del producto, esto significa que se multiplica el monomio por cada término del polinomio 
• Se efectúa el producto entre los monomios 
• Se ordena el polinomio
• Se coloca el monomio debajo del polinomio y luego se multiplica

Producto de polinomios

Para calcular el producto de polinomios se multiplica cada término de la expresión polinómica por cada uno de los términos de la otra expresión polinómica de igual manera como lo hace en la multiplicación de números enteros luego se suma las potencias de variable de exponentes iguales.

Pasos para multiplicar un polinomio por otro polinomio

• En primer lugar sino están ordenados se ordenan los polinomios de forma decrecienrte.
• Se multiplica cada término de un polinomio por el segundo polinomio se efectúa el producto entre los monomios.
• Se suman los términos semejantes

Propiedades de la multiplicación de polinomio

Propiedad conmutativa:

 Dado dos polinomio cualesquiera P(x)/Q(x) se cumple que P(x).Q(x)=Q(x).P(x)

Propiedad asociativa

Dados tres polinomios cualesquiera P(x), Q(x), y R(x)/Q(x), se cumple que P(x) [Q(x).R(x)]=[P(x).Q(x)]R(x)

Elemento neutro

Para todo polinomio Q(x)/Q, existe el polinomio unidad P(x)=1 / Q(x).1= 1.Q(x)= Q(x)

Propiedad distributiva de la multiplicación con respecto a la suma

Dado tres polinomio cualesquiera P(x), Q(x) y R(x) sobre Q, la propiedad distributiva establece que: P(x).[Q(x)+R(x)]=P(x).Q(x)+ P(x).R(x)

El rectángulo se ha dividido en cuatro figuras; calcula su área de formas: calculando el área del rectángulo grande y calculando el área de las cuatro figuras pequeñas y sumándose ¿qué observas en los resultados.

Para multiplicar polinomios debes multiplicar cada término de la expresión polinómica por cada uno de los términos de la otra expresión polinómica y luego sumar los términos de potencias iguales.

Ejemplo: dado los polinomios

  y

Debes un polinomio debajo del otro y se efectúa el producto de monomios de izquierda a derecha, quedando de la siguiente manera:

 Ejercicios resueltos de multiplicación de polinomios

Ejercicio # 1 Dado P(x) y Q(x)

Paso # 1 Ordenamos los polinomios de forma decreciente

 

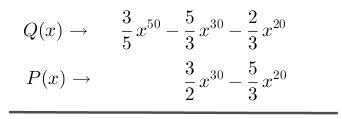
Paso # 2 Multiplicar el primer término del polinomio P(x) con el primer término del polinomio Q(x). Al multiplicar las fracciones simplifica el resultado hasta dejarlo a la mínima expresión

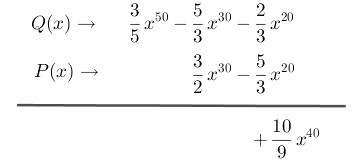
Paso # 3 Multiplica el primer término del polinomio P(x) con el segundo término del polinomio Q(x), siempre simplificando las fracciones

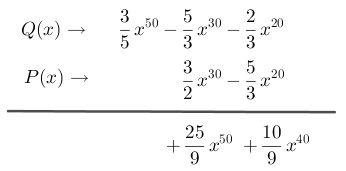
Paso # 4 Multiplica el primer término del polinomio P(x) con el tercer término del polinomio Q(x)

Paso # 5 Multiplica el segundo término del polinomio  P(x) con el primer término del polinomio Q(x), escribiéndolo en una segunda fila, el resultado se coloca en la columna con la variable del mismo exponente.

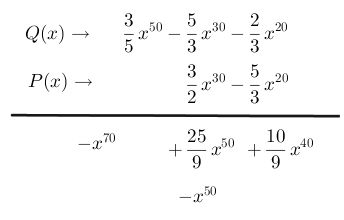
Paso # 6 Multiplica el segundo término del polinomio  P(x) con el segundo término del polinomio Q(x), escribiéndolo en la misma fila, el resultado se coloca en la columna con la variable del mismo exponente, en este caso este término queda en una columna sólo ya que en la fila de arriba no existe variable con exponente sesenta. Recuerde siempre simplificar las operaciones de las fracciones.

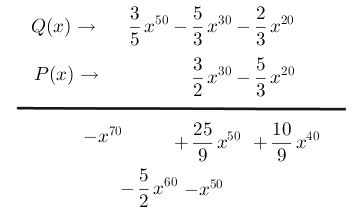
Paso # 7 Multiplica el segundo término del polinomio  P(x) con el tercer término del polinomio Q(x), escribiéndolo en la misma fila, el resultado se coloca en la columna con la variable del mismo exponente, en este caso este término queda en una columna sólo ya que en la fila de arriba no existe variable con exponente ochenta. Recuerda que siempre debes simplificar las operaciones de las fracciones.

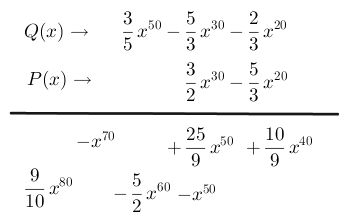
Paso # 8 Trazar una línea recta para comenzar a realizar la suma de los términos semejantes

Paso # 9 Sumar los términos semejantes de la primera columna

Paso # 10 Sumar los términos semejantes de la segunda columna

Paso # 11 Sumar los términos semejantes de la tercera columna

Paso # 12 Sumar los términos semejantes de la cuarta columna

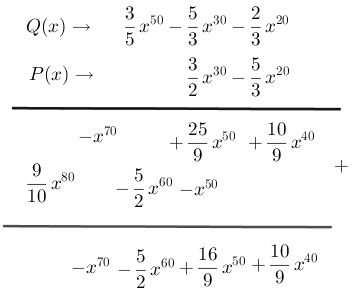
Paso # 13 Sumar los términos semejantes de la quinta columna y listo

Ejercicio # 2 Multiplique los polinomio P(x) y Q(x)

Paso # 1 Ordenamos los polinomios de forma decreciente

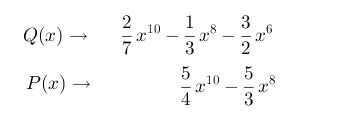
Paso # 2 Multiplicar el primer término del polinomio P(x) con el primer término del polinomio Q(x). Al multiplicar las fracciones simplifica el resultado hasta dejarlo a la mínima expresión.

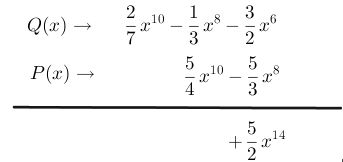
Paso # 3 Multiplica el primer término del polinomio P(x) con el segundo término del polinomio Q(x), siempre simplificando las fracciones

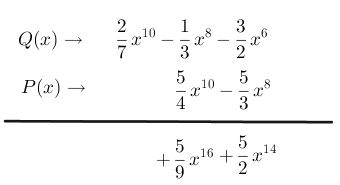
Paso # 4 Multiplica el primer término del polinomio P(x) con el tercer término del polinomio Q(x). Simplificando fracciones.

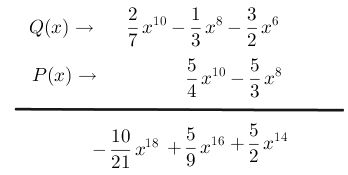
Paso # 5 Multiplica el segundo término del polinomio  P(x) con el primer término del polinomio Q(x), escribiéndolo en una segunda fila, el resultado se coloca en la columna con la variable del mismo exponente.

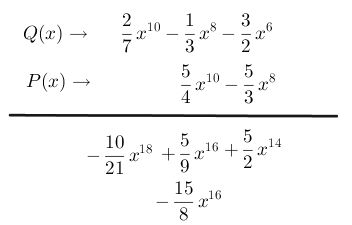
Paso # 6 Multiplica el segundo término del polinomio  P(x) con el segundo término del polinomio Q(x), escribiéndolo en la misma fila y en la columna correspondiente. Realice esto mismo hasta finalizar la multiplicación

Paso # 7 Trace una recta y sume todos los términos semejantes para obtener el resultado final