¿Te cuesta resolver división por Ruffini? Ya no tienes que preocuparte, cuando dividas por Ruffini ten en cuenta que un polinomio es una expresión algebraica que posee más de tres términos y que se encuentran en todo lo que haces en tu vida cotidiana. Por ejemplo, cuando vas al supermercado y clasificas las legumbres, hortalizas, verduras, carbohidratos y carnes, puedes ver que cada una de ellas representan variables que solo se pueden sumar o restar si son semejantes.

Para el  caso de operar la división por Ruffini lo puedes resolver de manera sencilla, sólo deberás tener en cuenta algunos pasos y podrás realizarlo de manera fácil y rápida. En esta oportunidad podrás ver cómo se divide utilizando la regla de Ruffini.

Antes de elaborar diferentes ejercicios es necesario que conozcas la  teoría, en el que conocerás los siguientes conceptos:

• Polinomio: es el que está formado por la suma o resta de varios monomios, un polinomio se puede dividir por un monomio o por otro polinomio.
• División: es una operación matemática, parcial y definida en el conjunto de los números naturales y los números enteros; en el caso de los números racionales, reales y complejos es siempre posible efectuar en la división, exigiendo que el divisor sea distinto.

Además de saber los conceptos de estos términos también es importante manejar las operaciones básicas con operaciones algebraicas, términos semejantes, suma, resta, multiplicación de fracciones. Ten en cuenta que el no manejar las operaciones básicas impedirán que avances en este contenido.

Ejercicio de dividir por Ruffini

Dividir un polinomio entre un  binomio de la forma (x-a)

Ejemplo: Dividir los polinomios P(x) y Q(x)

   y   

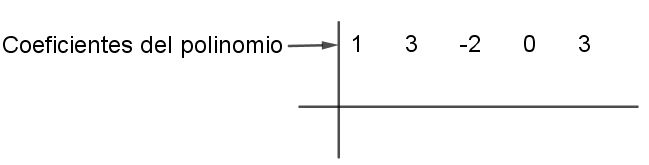
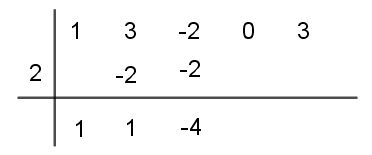
Paso # 1 Escribir en la primera fila los coeficientes del polinomio de manera ordenada y decreciente, escribiendo ceros en los lugares de los términos que faltan

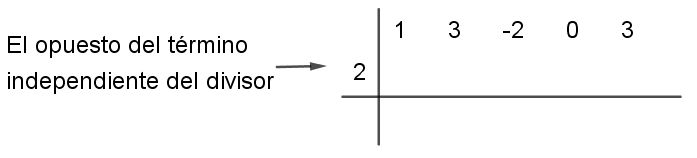
Paso # 2 Se escribe en la parte inferior izquierda el término independiente del divisor cambiando el signo, o lo que es lo mismo, el valor numérico de x que anula el divisor

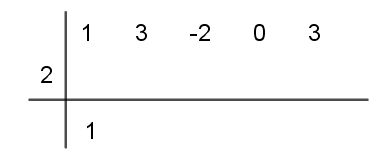
Paso # 3 El primer coeficiente del cociente es igual al primer coeficiente del dividendo

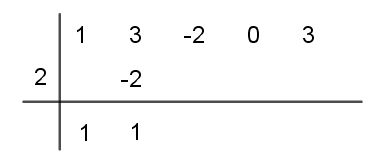
Paso # 4 El primer coeficiente del cociente, en este caso 1, se multiplica por (-2) y el producto resultante (-2) se suma al segundo coeficiente del dividendo, para obtener el segundo término del cociente. En este caso es 1

Paso # 5 La suma obtenida (1), la multiplicamos por (-2) y el producto resultante (-2) se suma al siguiente coeficiente (-2), obteniéndose (-4), el cual es el tercer término del cociente.

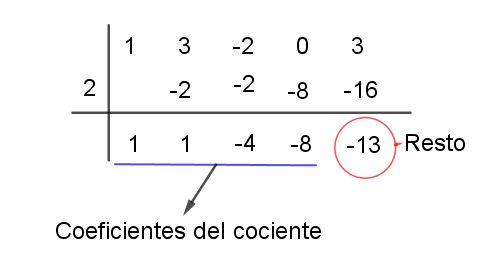
Pao # 6 Se continúa el proceso hasta efectuar la suma correspondiente al último coeficiente del dividendo. El número que queda situado a la derecha bajo la línea inferior, en este caso (-13), es el resto de la división.

Paso # 7 Los restantes números (1, 1, -4, y -8) son los coeficientes del polinomio

Paso # 8 Con los coeficientes formamos el polinomio resultante

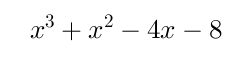
Dividir un polinomio entre un  binomio de la forma (ax+b)

Ejemplo: Dividir los polinomios P(x) y Q(x)

   y

Paso # 1 Transformar el divisor de la forma (x-a), se procede a dividir el dividendo y el divisor por 2, quedando así:

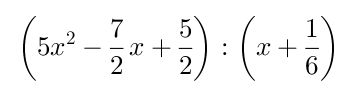
Paso # 2 Se realiza el mismo procedimiento del ejemplo anterior y resto se multiplica por 2, ya que este número fué el que se usó para llevarlo a la forma (x-a)

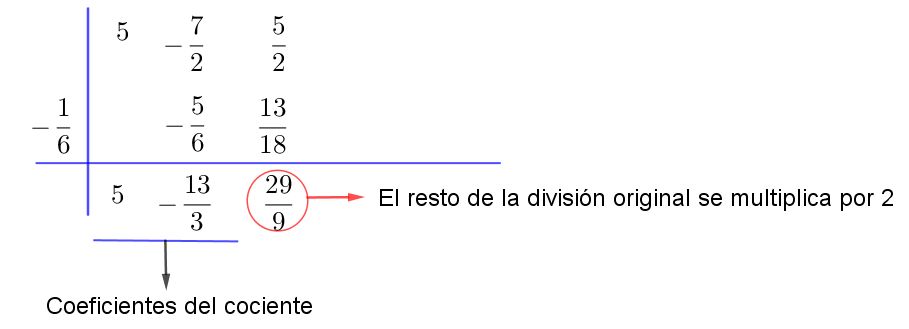
Paso # 3 Con los coeficientes formamos el polinomio resultante y el resto

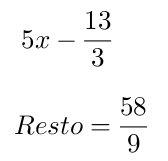
Dividir por Ruffini

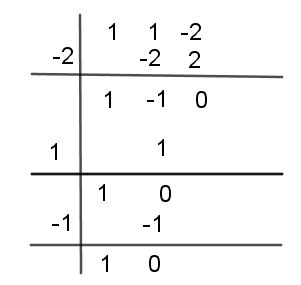
(x²+x-2) ÷ x-1

Pasos para resover por Ruffini

• Primero colocas la tabla donde reflejas el valor de X es decir en valor del número que está restando x como divisor. X vale 1.
• Luego, se colocan los coeficientes de polinomio ordenados del mayor al menor grado
• El primer número de arriba lo copias debajo de la línea.
• Se multiplica el número por el valor de X (1) y el resultado se coloca bajo el segundo número de arriba
• Se suman los dos números y repetimos la multiplicación expresando lo que dice la regla de Ruffini.
• La división de dos polinomios puede realizarse con mayor rapidez por ese procedimiento regla de Ruffini.
• Ahora sumamos los dos últimos números y ponemos el resultado abajo lo que sera el resto de la división.
• Se podrá construir el polinomio cociente de la división.
• En una división exacta de polinomios, el resto es igual a cero

Dividir el polinomio D(x) entre el polinomio D(x) es hallar otro polinomio cociente C(x) tal que multiplicado por el divisor de el dividendo.

D(x)=D(x). C(x)

Ejemplo:

x-1(x-1) No causa problemas porque el coeficiente dominante es 1.

División por un binomio

El cociente y el resto de una división de un polinomio con coeficiente entero en x entre x+a se pueden hallar usando la división larga de Ruffini.

Dividir polinomios

Es uno de los métodos que es más complejo y suele generar dudas ya que consiste en tomar en cuenta muchos conceptos que finalmente no se terminan de enterar por lo que es importante conocer monomios.

El proceso de división es más rápido por Ruffini, el primer paso es cuando la división  es de la forma x+a.

Método para dividir polinomio con una variable

• Se ordena el dividendo y el divisor según los polinomios decreciente de variable dividimos el término primero del dividendo entre el divisor, para obtener el primer número del cociente.
• Multiplicas el divisor por el primer término del cociente y lo restamos al dividendo  el resultado anterior para conseguir el primer resto parcial.
• Luego, repetimos  el procedimiento haciendo ahora el dividendo el primer resto parcial.
• La división finaliza cuando el grado del resto es menor que el grado del divisor.

Ejemplo

(6x³-2x)÷(4x+8)

Para realizar dicha división debemos cumplir las siguientes condiciones

1. Tanto dividendo (6x³-2x) como divisor (4x+8) deben tener la misma letra (en este caso la x)

2. El polinomio divisor (4x+8) debe ser de primer grado (la equis elevada a 1)

3. Los términos del polinomio dividendo (6x³-2x) debe estar agrupado de mayor a menor según el exponente.

4. El polinomio dividendo (6x³-2x) debe estar completo, según sea el exponente mayor ( en este ejemplo faltaría x² y el término independiente.

5. Si el polinomio divide (6x³-2x) no está completo  debe completarse con cero. En cuyo caso el polinomio dividendo (6x³-2x) debe quedar como 6x³+0x²-2x+0

Con el método de Ruffini, es muy particular del método de Horner en cuanto a la división y se utiliza es de primer grado de la forma x±b o en aquella división donde luego de un cambio de variable se obtiene un divisor de primer grado.