¿Sabes cómo factorizar polinomios? Resolver casos de factorización consiste en reunir un grupo de técnicas y luego convertir en producto el polinomio que tiene un grado menor que el grado del polinomio dado, en el que  se debe resaltar que unos de los casos de factorización que se utiliza es la regla de Ruffini. Además para factorizar se utilizan varios casos que verás en este artículo, nunca más tendrás problemas para factorizar.

Para factorizar polinomios aplicando el método de Ruffini es necesario aplicar los siguientes pasos:

1. Ordenar el polinomio en orden decreciente, en caso de que falte algún término dejamos el espacio o colocamos cero ya que el polinomio debe estar completo.
2. Se debe tomar en cuenta que tenga término independiente; si no lo tienes, sacar factor común hasta conseguir el término independiente.
3. Buscar todos los divisores del término independiente
4. Formar una tabla y colocar los coeficientes del polinomio
5. Colocar el primer divisor o raíz que se quiera usar en la esquina inferior izquierda, y baja el primer coeficiente tal cual esté. Para la selección de división debes tener presente que los números que vas obteniendo o bajando los vas a multiplicar por el divisor y el resultado de la multiplicación lo vas a sumar o restar con los coeficientes que tienes; el divisor que se escoja debe ser un número que haga que al final dé como resto cero. Para saber si un número es raíz; es sustituyendo en el polinomio ese número como el valor de la variable (x), y si da cero (0) es raíz, si no da cero no lo es y se pasa al siguiente divisor.
6. Al obtener la primera raíz el proceso se respeta con los nuevos coeficientes obtenidos hasta que quede un solo coeficiente o hasta que no exista ninguna raíz que haga que nos de cero (0).

Factorización por factor común

5x+25

Paso #1 En primer lugar debes hacer el proceso inverso de la propiedad distributiva, quedando el factor común de la siguiente forma:

5x+25 = 5(x+5)

Factorizar polinomios por agrupación

La factorización por agrupación es una doble factorización de factor común.

xy +4y+5x+20=

Para resolver esta factorización se destacan los términos comunes, quedando de la siguiente manera:

   xy+4y+5x+20 

   =y(x+4) +5(x+4)

Si observas el polinomio resultante tiene términos comunes que es x+4 quedando de la siguiente manera:

(y+5)(x+4)

Trinomio cuadrado perfecto

Para saber si se trata de un trinomio cuadrado perfecto debes hallar la raíz cuadrada del primer término y tercer término (25). Luego, ambas raíces resultantes al multiplicar por 2 debe ser igual al segundo término.  

                 x²+10x+25

              = (x+5) (x+5)

Factorizar polinomios por diferencia de cuadrados

La diferencia de cuadrados es el producto de dos binomios con un primer término y un segundo término iguales pero con signos opuesto. A continuación, aquí tienes un ejemplo:

(x-5) (x+5)

= x²-5

 = x²-25

Factorizar polinomios por Ruffini

La factorización de polinomios por Ruffini consiste en escribir los polinomios en forma de factores.

Ejemplo:

x⁴-10x³+35x²-50x+24=0

Quiere decir que sustituimos a x por 1, 2, 3,4 y su resultado será igual a cero, se puede decir:  x=1; x=2; x=3; x=4; lo que queda así haciendo sustitución:

(x-1)=0; (x-2)=0; (x-3)=0;(x-4)=0

Esto se refiere a escribir los polinomios en forma de factores.

Factorización de la forma Ax²+Bx+C

3x²+9x+6=0

Paso 1: Divides entre 3 ya que todos los términos son divisibles entre 3

(3x²+9x+6)/3= x²+3x+2=0

Paso 2. Posteriormente se buscan dos números que multiplicados el resultado sea 2 y sumado dé 3, quedando de la siguiente manera:

(x+1)(x+2)

Solución

El polinomio esta ordenado completo y tiene término independiente.

Los divisores del término independiente D(6)=±1±2±3±6 bajamos los coeficientes y formamos la tabla

+3  +9  +6

+1      +3  +12

+3  +12  +18

Se probó con el (+1) y dio resto igual a 1 (18) porque (1*3=3) (3+9=12) (1*12=12) (12+6=18);por lo tanto podemos decir que este divisor no nos sirve .

Ejercicios

Factorizar polinomios

P(x)=x⁴ -9x³+4x²+12x

1. Factor común

Todos los términos tienen x, es un factor común

x(x³-9x²+4x+12), ya se tiene un factor que es x para comprobar que esta buen hecho  al multiplicar debe obtener P(x)

2. Ruffini se aplica sustituimos la x del polinomio.

Veamos en el siguiente ejercicio de polinomio, de grado 2 (cuadrático) que no se puede descomponer como producto de polinomios reales de grado 1.

No se puede hacer porque los factores cuadráticos irreducibles en la factorización de un polinomio real cualquiera, vienen dadas por el producto de dos polinomios de primer grado con raíces imaginarias conjugadas.

Factoriza el polinomio P(x)=x⁴+2x²+1 en términos de factores cuadráticos irreducibles

Factoriza el polinomio  P(x)= 3x⁴+3x³+3x²-3x²+3x-6 en términos  de primer grado y cuadráticos irreducibles.

Teorema del resto es muy importante conocer en que consiste ya que en dicha teoría  el valor numérico del dividendo compagina con el valor del resto para aquellos valores de x que no anulan la división por Ruffini.

Factorizar polinomios

    x³+6x²+4x+6

Paso #1 Aplicando la Regla de Ruffini

    x³+6x²+4x+6

Paso #1 Tomar los coeficientes y organizar para aplicar Ruffini, tal como lo ves en la imagen. Pruebas con los divisores de 6, en este caso comienzas con (-2)

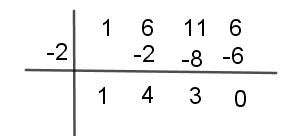
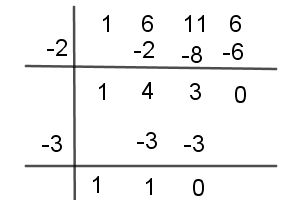
Paso #3 Por último, utilizas el divisor (-1)

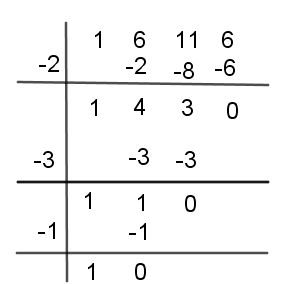
Paso #4 Finalmente, se obtiene el polinomio factorizado de la siguiente manera:

Un polinomio puede tener tantos factores como su grado.

Ahora ya conociendo para que sirva el teorema del resto podemos factorizar  un polinomio aplicando la teoría del resto.

Si dividimos p(x): (x-a) y la división es exacta:

P(x) entre x-a=q(x)

Entonces P(x)=(x-a).q(x)

Se puede decir que: x-a es una raíz 0 cero de polinomios P(x)

Teorema

P(x) es un polinomio con coeficientes enteros y x-a es un cero entero del polinomio x-a, entonces x-a divide el término independiente del polinomio p(x) para factorizar polinomios.

4. Factorizar polinomios con el trinomio cuadrado perfecto

x²+8x+16

Solución

Paso #1 Lo primero que debes saber es si la expresión se trata de un trinomio cuadrado perfecto. Esto quiere decir si el primer caso y el último son cuadrados perfecto, quedando de la siguiente manera:

x²+8x+4²

Paso #2 Seguidamente compruebas que el término medio es el doble producto de las raíces cuadradas del primero y el último término, quedando de la siguiente forma:

x²+2.4.x+4²

Paso #3 Esto significa que queda factorizado:

x²+8x+16= (x+4)²