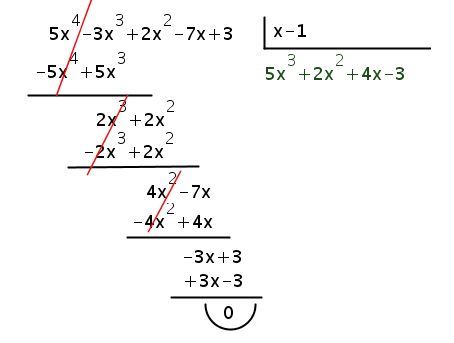
¿La división de polinomios es tu dolor de cabeza? Para resolver este tipo de ejercicios lo primero que debes saber es que se deben ordenar en forma decreciente, con respecto a una misma variable y en el mismo sentido en orden ascendente o descendente, si el polinomio no es completo se deja los espacios de los términos que faltan. Así que no busques y pon manos a la obra, dividir polinomios será una gran experiencia.

 Pasos para resolver la división de polinomios

• El primer término del cociente se obtiene dividiendo el primer término del divisor, se multiplicará el primer término del cociente para todos los términos del divisor, se coloca este producto debajo del dividendo y se resta al dividendo.
• El segundo término del cociente se obtiene dividiendo el primer término del dividendo parcial o resta entre el primer término del dividendo, se multiplica el segundo término del cociente por los términos del divisor, se coloca este producto del dividendo parcial y se resta del dividendo parcial.
• Continúa de esta manera hasta que el resto sea cero o un dividendo parcial cuyo primer término me pueda ser dividido por el primer termino del divisor.

División de polinomios entre monomios

Para dividir un polinomio entre un monomio se distribuye el polinomio sobre el monomio se realiza convirtiéndolo en fracciones.

1. Coloca el monomio como denominador del polinomio
2. Separa el polinomio en diferentes términos separados por el signo y cada uno dividido por el monomio.
3. Se realizan las respectivas divisiones entre monomios tal como se realizó anteriormente.
4. Se realizan las sumas y restas necesarias.

Propiedades de la división de polinomio

Partes que forman cualquier división, sea una división entre números o entre polinomios, estará formada por el dividendo, el divisor, el cociente y el resto

Si estas partes las escribes  en forma de polinomio, queda

D(x)÷ d(x)

R(x)    C(x)

Y cumplen las siguientes propiedades:

• El grado del dividendo D(x) es mayor o igual que el grado del divisor d(x):

Grado D(x)≥ Grado d(x).

•  El grado del dividendo D(x) es igual al grado del divisor d(x) más el grado del cociente C(x):

Grado D(x)=Grado d(x)+Grado C(x).

•  El grado del resto R(x) es menor que el grado del divisor d(x):

Grado R(x)<Grado d(x).

• El dividendo es igual al divisor por el cociente más el resto:

D(x)=d(x).C(x)+R(x), al comprobar esta fórmula con una división de números comprobarás que también se cumple.

Dividir polinomios utilizando la regla de Ruffini

También es importante recalcar, que existen varios métodos para obtener métodos para dividir polinomios, uno de los más nombrados es el método o regla de Ruffini, cuyo método sirve para dividir cualquier tipo de polinomios para los que hay que tener en cuenta las propiedades que trabajos anteriormente.

Ejemplo:

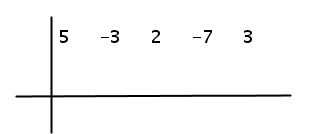
Paso #1 Ordenar el polinomio en forma decreciente y colocar los coeficientes

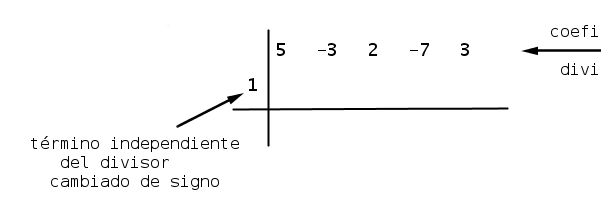
Paso #2 Colocas el término independiente como es x-1, entonces colocas +1

Paso #3 Bajar el primer término (5), luego multiplica el 1 por cada uno de los coeficientes y finalmente suma o resta según sea el caso.

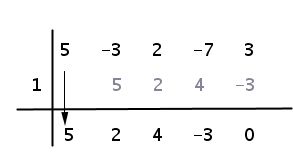
Paso #4 Finalmente se obtiene el resto de la división que es el cero y los que están antes representan los coeficientes como lo ves en la imagen.

 

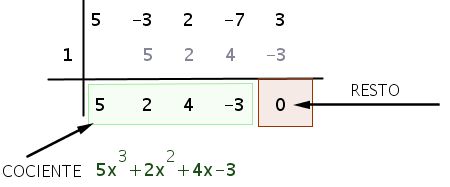
División de polinomio de forma clásica

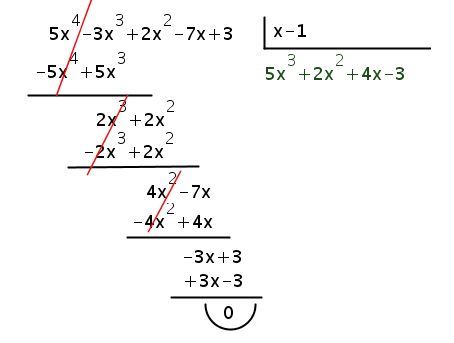
El primer paso consiste en colocar y escribir correctamente el dividendo y el divisor para realizar la división en dicho caso en numerador es el dividendo y el denominador es el divisor, tanto en el dividendo como el divisor los términos se escriben en orden de creciente de los grados de sus términos, es decir empezar por el mayor grado, el término de grado cero (término independiente).

Si falta el término de algún grado en el dividendo se deja un espacio en su lugar en el ejemplo que veremos a continuación, el dividendo no tiene termino de grado dos por lo que se deja un espacio.

Finalizado este procedimiento en su serie el dividendo y el divisor, y con los espacios correspondientes de los términos que faltan se empieza a resolver el cociente por lo que dividimos el primer término del dividendo entre el primer término del divisor .

Y lo colocamos en el cociente correspondiente al primer término del cociente:

Luego se multiplica este término del cociente por cada uno de los términos del divisor.

Métodos para dividir polinomios con una variable.

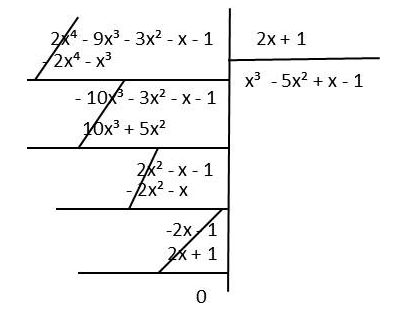
Paso # 1 En primer lugar se ordena el dividendo y el divisor según las potencias decrecientes de la variable. Si observas el polinomio planteado en la imagen está completo y está ordenado en forma decreciente, en ese caso puedes proceder a resolver de inmediato.

Paso #2 Procede a dividir el término primero del dividendo entre el termino primero del divisor, para obtener el primer término del cociente. En este caso, resulta:

2x⁴÷2x= x³

Paso # 3 Multiplicas el divisor por el primer término del cociente y le restas el dividendo el resultado anterior para conseguir el primer resto parcial.

Paso #4 Repites  el procedimiento haciendo ahora, dividiendo el primer resto parcial

Paso #5 La división finaliza cuando el grado del resto es menor que el grado del divisor.

Es importante que tengas en cuentas que el cociente y el resto de una división de un polinomio con coeficientes enteros en x entre x+a se pueden hallar usando la división larga o utilizando la regla de Ruffini. Teniendo en cuenta que  la propiedad del  cociente de esta división será un polinomio en x cuyo grado es una unidad menor que el grado del dividendo y cuyo coeficiente general del cociente es igual al coeficiente del término general del dividendo.

La división de un polinomio por un monomio se obtiene dividiendo cada termino del polinomio por el monomio, obteniendo como resultado otro polinomio.

Cuando lo anterior no es posible, se puede simplificar pero el segundo término y el tercero no se pueden dividir. Ya para finalizar es importante denotar que al dividir  polinomios debemos tomar en cuenta que está formado por las sumas o resta de varios monomios, un polinomio puede dividirse por un monomio o por otro polinomio,  es algo complejo pero si se puede realizar.