¿Sabes cómo hacer Ruffini? Para realizar ejercicios de factorización de polinomios es importante conocer  Ruffini y para ello es primordial saber en detalle en qué consiste su regla. La mayoría de los estudiantes elige este método para factorizar debido a que permite solucionar ecuaciones de tercer grado o mayor, dividir polinomios entre binomios y factorizar polinomios con grados mayor a tres de forma rápida.

¿Qué ejercicios puedes resolver con la regla de Ruffini?

1. Resolver ecuaciones de 3 grado o mayor (cuarto y quinto grado)
2. Dividir un polinomio entre un binomio que sea de forma (x-2)
3. Factorizar polinomios de tercer grado o mayor (cuarto grado, quinto grado)
4. Calcular las raíces de polinomios de grado mayor o igual a 3.

Aplicar Ruffini consiste en la descomposición de un polinomio de grado (n) y convertirlo en un binomio y otro polinomio de grado (n-1) para lo que es importante conocer por lo menos 1 de las raíces del polinomio dado.

Para la aplicación del mismo es necesario  que el polinomio dado tenga termino independiente y si no lo tiene se debe sacar factor común, tantas veces como sea necesario hasta dejar un polinomio con términos independientes.

El procedimiento para hacer Ruffini

Se multiplica la primera raíz por el primer coeficiente que es el que debes  bajar, luego el resultado de la multiplicación se va a sumar o restar con el siguiente coeficiente.

Seguidamente el resultado de la operación algebraica se va multiplicar con la raíz, y el resultado de la multiplicación, se le suma o resta al siguiente coeficiente; dicho resultado de la operación algebraica se multiplica con la raíz y el resultado de la multiplicación se le suma o resta el siguiente coeficiente, todo esto se repite hasta llegar al último coeficiente y en ese coeficiente se obtiene un resto igual a cero si esto no sucede la raíz no es correcta, entonces debes hacer la prueba con otro divisor .

Para aplicar Ruffini es muy importante que en la práctica logres  entender lo siguiente:

x³-3x-2= 0

El polinomio es de grado 3 y se escribe en la primera fila los coeficientes de cada monomio en orden decreciente de grado, si hay algún coeficiente que sea cero (0) en este caso es el coeficiente de x² también hay que escribirlos.

La regla de Ruffini establece un método para la división de polinomios que también es de gran importancia recalcarlo en este momento como lo es la división de polinomios como se aplica mediante el método de Ruffini:

• Se trazan dos líneas a en forma de eje y se escribe los coeficientes de p(x), ordenados y sin omitir términos nulos se escribe la raíz r del lado de la izquierda invirtiendo el signo de este y el primero coeficiente en el signo inferior (an)
• Se multiplica (an) por r y se escribe debajo de an-1
• Se suma los dos valores obtenidos en la misma columna
• En este paso se repite el procedimiento
• Los valores de b son los coeficientes del polinomio
• Resultante R(x) de grado uno menos que el grado de p(x)
• El resultado es S

En cuanto a la solución de las ecuaciones nos referimos a los valores numéricos de la ecuación (variable -incógnita) para los cuales la igualdad es cierta, es decir sustituir valores por letras en la ecuación y al obtener una igualdad Ejemplo de ecuación 5x-3=7

También es importante establecer las relaciones en la regla de Ruffini

La relación es la siguiente:

• A`=A es decir el primer coeficiente del cociente A es igual al primer coeficiente del dividendo A
• B`=Aa+B es decir el segundo coeficiente del cociente B` se obtiene mediante la relación B=Aa+B
• C`=Ba+C es decir el tercer coeficiente del cociente C` se obtiene mediante la relación C`=B`a+C
• R=C`a+D es decir el resto R se obtiene mediante la relación R=C`a+D

Ejercicios resueltos

Ruffini estableció un útil algoritmo para calcular el cociente y el resto (x-x)

Vamos a explicar como trabaja y luego justifica remos su idea .supongamos que queremos dividir

P(x)=x⁴- 3x³+5x²-7x+9  por (x-2).

Paso #1 En primer lugar procede a colocar  los coeficientes de p(x) en el  arreglo como el que ves a continuación. Si alguna potencia de x falta se coloca cero.

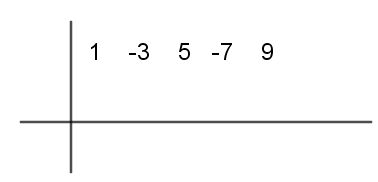
Paso #2 Seguidamente, coloca 2 el cual se multiplicará por  cada uno de los coeficientes

 

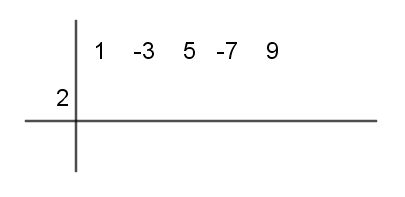
Paso #3 Luego, se multiplica el 2 por 1 (el que está bajo la línea) y lo colocamos debajo del  (-3).

 

Paso #4. Además, sumas -3+2=-1 y el resultado se escribe  debajo la línea.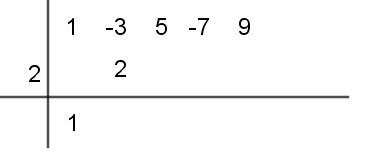

Paso #5 Ahora  multiplicas el -1 por 2, escribimos el resultado bajo el 5, y calculamos 5-2=3. Este resultado se escribe bajo la línea. Reiteramos este proceso pero ahora con el 3 : lo multiplicamos por el dos, escribimos este resultado bajo el -7 y calculamos -7 +6=-1

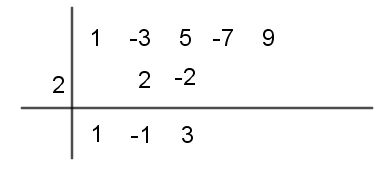
Paso #6 Reiteramos este proceso pero ahora con el 3 : lo multiplicamos por el dos, escribimos este resultado bajo el -7 y calculamos -7 +6=-1. Finalmente, multiplicamos -1 por 2, lo escribimos bajo el 9 ,y calculamos 9-2=7. El cual  copiamos bajo la línea.

El resto de la división corresponde al último término, es decir al que aparece después de la línea, en este caso 7. El polinomio cociente c(x) está determinado por el resto de los coeficientes que aparecen en la última fila, tomados como coeficientes del cociente escrito con potencias de x  decrecientes. En este caso:

C(x)=x³-x²+3x-1

Una observación muy útil es que el método de Ruffini nos da una manera alternativa de comprobar el resultado es susituir el 2 en la expresión polinómica. Tal como lo observas a P(2)=2⁴-3.2³+5.2²-7.2+9=16-24+20-14+9=7

Cómo hacer Ruffini en    x³+6x²+11x+6

Para resolver el siguiente polinomio aplicando Ruffini, seguir los siguientes pasos:

Paso#1 Tomar los coeficientes de la expresión polinómica y colocar en la tabla de Ruffini

Paso#2 Utiliza los divisores uno por uno para conseguir la primera raíz, tal como la ves en la imagen. Ten en cuenta bajar el primer coeficiente de izquierda a derecha, en este caso es 1.

Paso#3 Seguidamente, procede a sumar las columnas del resultado de multiplicar (-2).1

Paso #4 Continúa realizando el mismo proceso hasta obtener cero (0) en el último término

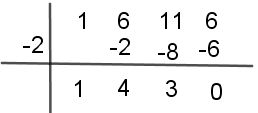
Paso #5 Repite el proceso anterior con el otro divisor hasta lograr que el último término sea cero (0)

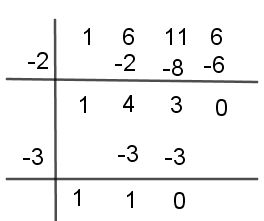
Paso #6 Repite el proceso con el siguiente divisor

Paso #7 Ahora que sabes cómo hacer Ruffini, te queda el polinomio factorizado de la siguiente manera: